Предмет: Математика,
автор: Знания
Угол между биссектрисой и медианой прямоугольного треугольника, проведенным из вершины прямого угла равен 21 градус.
Найдите меньший угол этого треугольника.
Ответ дайте в градусах
Прошу подробный ответ со всеми объяснениями и чертежом.
Ответы
Автор ответа:
0
По свойству медианы в равнобедренном треугольнике:
Медиана в прямоугольном треугольнике, проведённая из прямого угла к гипотенузе равна её половине.
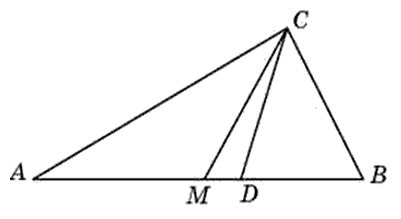
1) Рассмотрим ΔACM - он равнобедренный где AM=MC
а значит ∠CAM=∠ACM
Из ΔACD где CD= биссектриса ΔABC можно найти ∠ACM
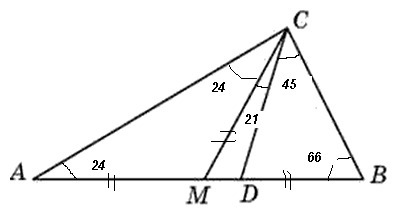
∠ACM=∠АCD-∠MCD=45°-21°=24°
т.к. ∠CAM=∠ACM=24°
Сумма углов ΔABC=180°. значит ∠CBA=180°-24°-90°=66°
Меньший угол = 24°
2) Можно рассмотреть и другой случай:
Рассмотрим ΔMCB
он равнобедренный где MC=MB
отсюда ∠MCB=∠CBM
∠MCB=45°+21°=66°=∠CBM
А значит ∠CAB=180°-90°-66°=24°
Приложения:
Автор ответа:
0
Отлично!
Автор ответа:
0
"∠ACM=∠FCD-∠MCD". Что за F?
Автор ответа:
0
Простите, опечатка
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Литература,
автор: abdull24011978
Предмет: Математика,
автор: Accivhonda3
Предмет: География,
автор: Котя1200
Предмет: Литература,
автор: СаНдОрИк