Предмет: Геометрия,
автор: natalie17wow
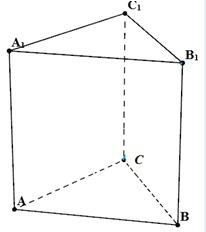
ΔABC со сторонами 10, 17 и 21, является основанием прямой призмы ABCA1B1C1. Площадь основания призмы равна площади наименьшей боковой грани. Найдите объем призмы.
Приложения:
Ответы
Автор ответа:
0
Площадь основания найдём по формуле Герона: S=√(p(p-a)(p-b)(p-c)), где р=(a+b+c)/2=(10+17+21)/2=24.
S=√(24(24-10)(24-17)(24-21))=84.
Так как все боковые грани равны, то гранью с наименьшей площадью будет грань с наименьшей стороной из основания призмы, то есть 10.
Площадь этой грани: 84=10·h ⇒ h=84/10=8.4
Объём призмы: V=Sh=84·8.4=705.6 (ед³).
S=√(24(24-10)(24-17)(24-21))=84.
Так как все боковые грани равны, то гранью с наименьшей площадью будет грань с наименьшей стороной из основания призмы, то есть 10.
Площадь этой грани: 84=10·h ⇒ h=84/10=8.4
Объём призмы: V=Sh=84·8.4=705.6 (ед³).
Похожие вопросы
Предмет: Геометрия,
автор: sdsfgdfgfdgdfgfdgd
Предмет: Геометрия,
автор: anfisalevchenko
Предмет: Математика,
автор: kravcenkoalina25
Предмет: Биология,
автор: polinavetka
Предмет: Биология,
автор: polinavetka