Предмет: Математика,
автор: Аноним
Найдите площадь фигуры ограниченной линиями y = 2+x(в степени )2 и у = 4 – х
Ответы
Автор ответа:
0
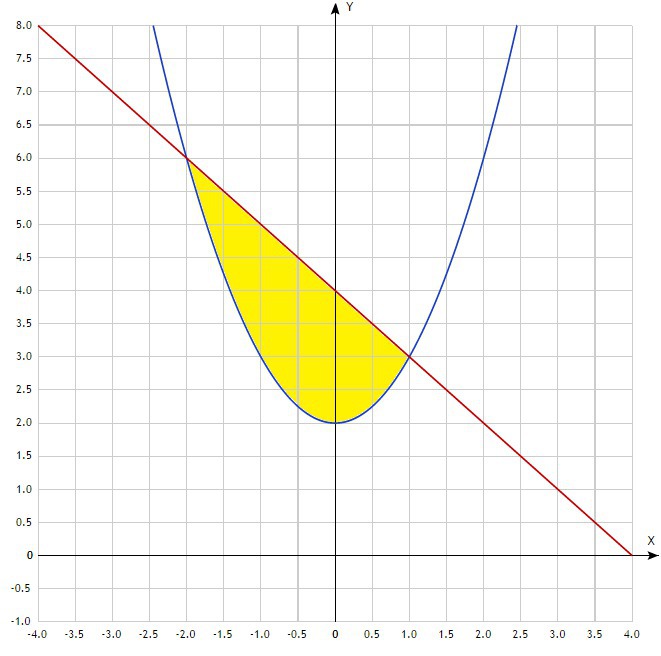
Чертим чертёж. По нему видно, что на промежутке [-2;1] расположена наша фигура и сразу становится понятно какая функция больше на этом промежутке, а именно y=4-x больше y=2+x². Точки пересечения графиков можно найти и аналитически, решив уравнение:
2+x²=4-x
x²+x-2=0
D=1²-4*(-2)=9
x=(-1-3)/2=-2 x=(-1+3)/2=1
Далее вычисляем определённый интеграл, что в геометрическом смысле и есть вычисление площади


 ед².
ед².
2+x²=4-x
x²+x-2=0
D=1²-4*(-2)=9
x=(-1-3)/2=-2 x=(-1+3)/2=1
Далее вычисляем определённый интеграл, что в геометрическом смысле и есть вычисление площади
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: vernickaaasa710
Предмет: Литература,
автор: bezkorovajnaaviolett
Предмет: Физика,
автор: Vikaorazmedova
Предмет: Математика,
автор: begeiirina111