Предмет: Алгебра,
автор: Motamka
решите уравнение, пожалуйста
Приложения:
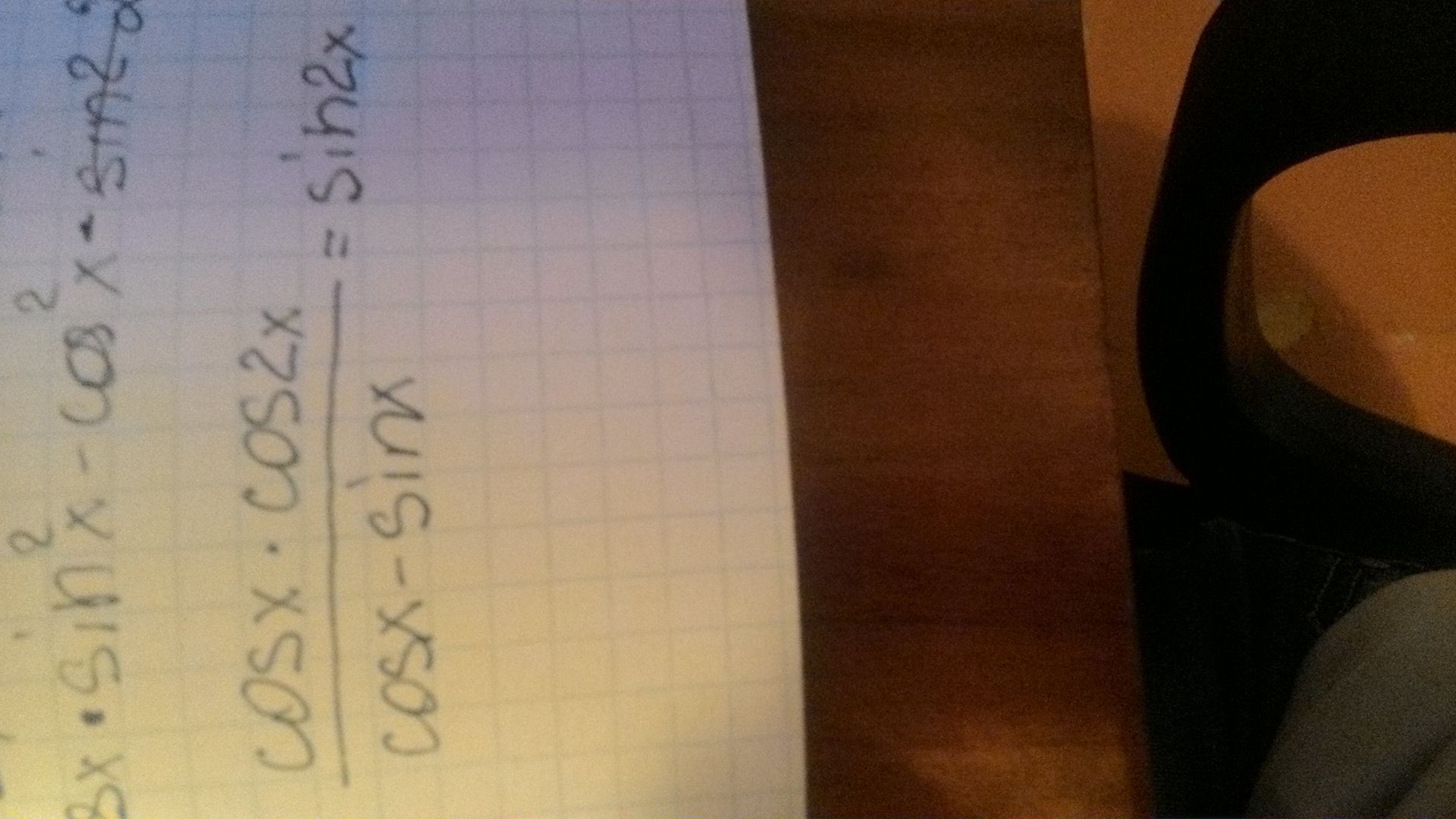
Ответы
Автор ответа:
0
ОДЗ: Cosx-Sinx≠0
1-tgx≠0
tgx≠1
x≠ (n∈z)
(n∈z)

Cosx=0 или Cosx-Sinx=0 I :Cosx≠0
x= +
+ или 1-tgx=0
или 1-tgx=0
С первым случаем все понятно, потому я распишу второй
tgx=1
x= /4+
/4+ не удовлетворяет ОДЗ
не удовлетворяет ОДЗ
Ответ: +
+  n (n∈z).
n (n∈z).
1-tgx≠0
tgx≠1
x≠
Cosx=0 или Cosx-Sinx=0 I :Cosx≠0
x=
С первым случаем все понятно, потому я распишу второй
tgx=1
x=
Ответ:
Автор ответа:
0
во второй строчке вы сократили на cosx-sinx, значит в третьей у вас должно быть cosx(cosx+sinx)=sin2x
Автор ответа:
0
спасибо, что нашли ошибку, я была невнимательна в учете ОДЗ и в той строчке.
Автор ответа:
0
исправьте, пожалуйста, или ответ придется удалить
Автор ответа:
0
всё
Автор ответа:
0
ОДЗ: cosx-sinx≠0 |:cosx
1-tgx≠0
tgx≠1
x≠(π/4) +πn, n∈Z


не удовлетворяет ОДЗ

n∈Z
1-tgx≠0
tgx≠1
x≠(π/4) +πn, n∈Z
не удовлетворяет ОДЗ
n∈Z
Похожие вопросы
Предмет: Математика,
автор: maksimka2578944
Предмет: Математика,
автор: dashynaket2
Предмет: Английский язык,
автор: baikovdaniil4
Предмет: Химия,
автор: ramilya1997
Предмет: История,
автор: кешеко55587