Предмет: Математика,
автор: маринька
помогите срочно решить уравнение
Приложения:
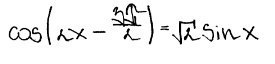
Ответы
Автор ответа:
0
cos(2x-3π/2)=sin2x
sin2x-√2sinx=0
2sinxcosx-√2sinx=0
sinx(2cosx-√2)=0
sinx=0⇒x=πn,n∈z
cosx=√2/2⇒x=+-π/4+2πk,k∈z
sin2x-√2sinx=0
2sinxcosx-√2sinx=0
sinx(2cosx-√2)=0
sinx=0⇒x=πn,n∈z
cosx=√2/2⇒x=+-π/4+2πk,k∈z
Автор ответа:
0
а там минуса перед sin2x не должно быть?
Автор ответа:
0
минус должен быть
Автор ответа:
0
-sin2x=√2sinx по формуле приведения
√2sinx+sin2x=0
√2sinx+2sinxcosx=0
√2sinx(1+√2cosx)=0
a) sinx=0 b)1+√2cosx=0
a) x=πn, n -целое; b) cosx=-1/√2⇒x=(π-π/4)+2πk⇒x=(3π/4)+2πk, k-целое
√2sinx+sin2x=0
√2sinx+2sinxcosx=0
√2sinx(1+√2cosx)=0
a) sinx=0 b)1+√2cosx=0
a) x=πn, n -целое; b) cosx=-1/√2⇒x=(π-π/4)+2πk⇒x=(3π/4)+2πk, k-целое
Похожие вопросы
Предмет: Алгебра,
автор: vikatrvka
Предмет: Математика,
автор: Аноним
Предмет: Геометрия,
автор: dasasocka11
Предмет: История,
автор: акция
Предмет: Алгебра,
автор: annastalker99