Предмет: Математика,
автор: mironov1311
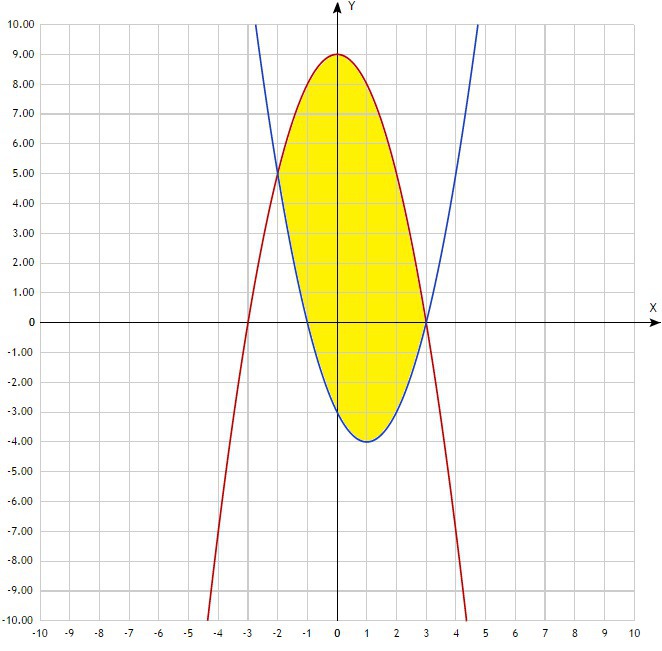
Найдите площать фигуры, ограниченной линиями y=9-x^2, y=x^2-2x-3
Ответы
Автор ответа:
0
Делаем чертёж. По нему определяем, что функция y=9-x² больше функции y=x²-2x-3 на промежутке [-2;3] (абсциссы точек пересечения графиков функций). Данные точки (пределы интегрирования) можно найти и аналитически приравняв обе функции:
9-x²=x²-2x-3
x²+x²-2x-3-9=0
2x²-2x-12=0 |:2
x²-x-6=0
D=(-1)²-4*(-6)=1+24=25
x=(1-5)/2=-2 x=(1+5)/2=3
Площадь фигуры вычисляется путём вычисления определённого интеграла по формуле:



 ед²
ед²
9-x²=x²-2x-3
x²+x²-2x-3-9=0
2x²-2x-12=0 |:2
x²-x-6=0
D=(-1)²-4*(-6)=1+24=25
x=(1-5)/2=-2 x=(1+5)/2=3
Площадь фигуры вычисляется путём вычисления определённого интеграла по формуле:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: kstwrt
Предмет: Английский язык,
автор: voloshinav59
Предмет: Физкультура и спорт,
автор: Ivleevajulia2004
Предмет: Алгебра,
автор: ИронияБитчез
Предмет: Литература,
автор: vvelichko1978