Предмет: Математика,
автор: Eminem1614
Уравнение , найдите решение 2sin^2 x - 5cos x - 5 = 0
Условие удовлетворяющее sin x > 0
Ответы
Автор ответа:
0
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:
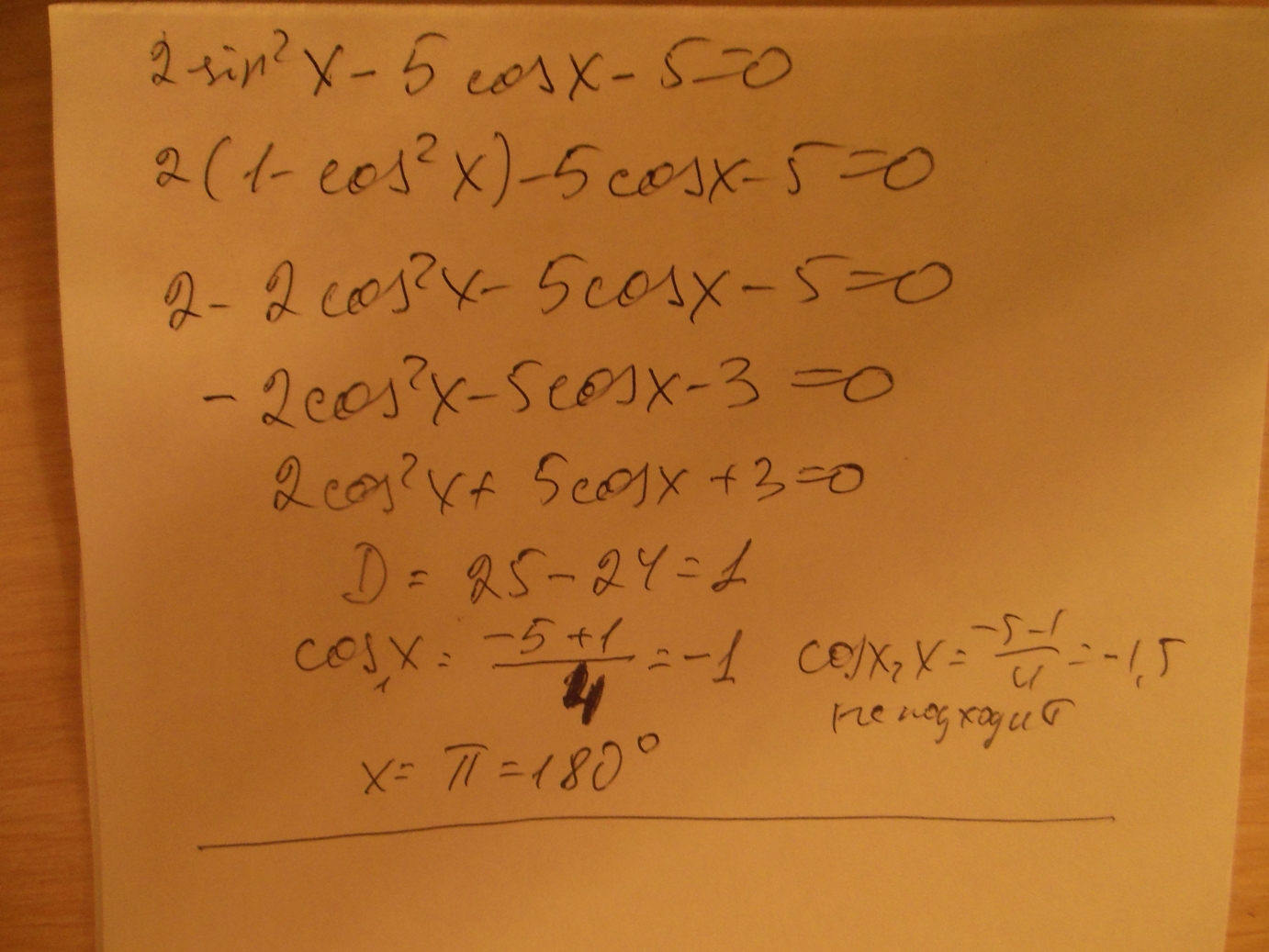
Автор ответа:
0
Дано уравнение 2sin^2 x - 5cos x - 5 = 0.
sin²x = 1 - cos²x.
Тогда 2(1 - cos²x) - 5cos x - 5 = 0,
2 - 2cos²x - 5cosx - 5 = 0.
2cos²x + 5cosx + 3 = 0. Замена: cosx = t.
Имеем квадратное уравнение:
2t² + 5t + 3 = 0.
Квадратное уравнение, решаем относительно t:
Ищем дискриминант:D=5^2-4*2*3=25-4*2*3=25-8*3=25-24=1;
Дискриминант больше 0, уравнение имеет 2 корня:t_1=(√1-5)/(2*2)=(1-5)/(2*2)=-4/(2*2)=-4/4=-1;t_2=(-√1-5)/(2*2)=(-1-5)/(2*2)=-6/(2*2)=-6/4=-1,5 этот корень отбрасываем.
Обратная замена cosx = -1.
х = π + 2πk, k ∈ Z.
Так как sin (π + 2πk) равен 0, то условие, удовлетворяющее sin x > 0 не найдено. Задача не имеет решения.
sin²x = 1 - cos²x.
Тогда 2(1 - cos²x) - 5cos x - 5 = 0,
2 - 2cos²x - 5cosx - 5 = 0.
2cos²x + 5cosx + 3 = 0. Замена: cosx = t.
Имеем квадратное уравнение:
2t² + 5t + 3 = 0.
Квадратное уравнение, решаем относительно t:
Ищем дискриминант:D=5^2-4*2*3=25-4*2*3=25-8*3=25-24=1;
Дискриминант больше 0, уравнение имеет 2 корня:t_1=(√1-5)/(2*2)=(1-5)/(2*2)=-4/(2*2)=-4/4=-1;t_2=(-√1-5)/(2*2)=(-1-5)/(2*2)=-6/(2*2)=-6/4=-1,5 этот корень отбрасываем.
Обратная замена cosx = -1.
х = π + 2πk, k ∈ Z.
Так как sin (π + 2πk) равен 0, то условие, удовлетворяющее sin x > 0 не найдено. Задача не имеет решения.
Приложения:
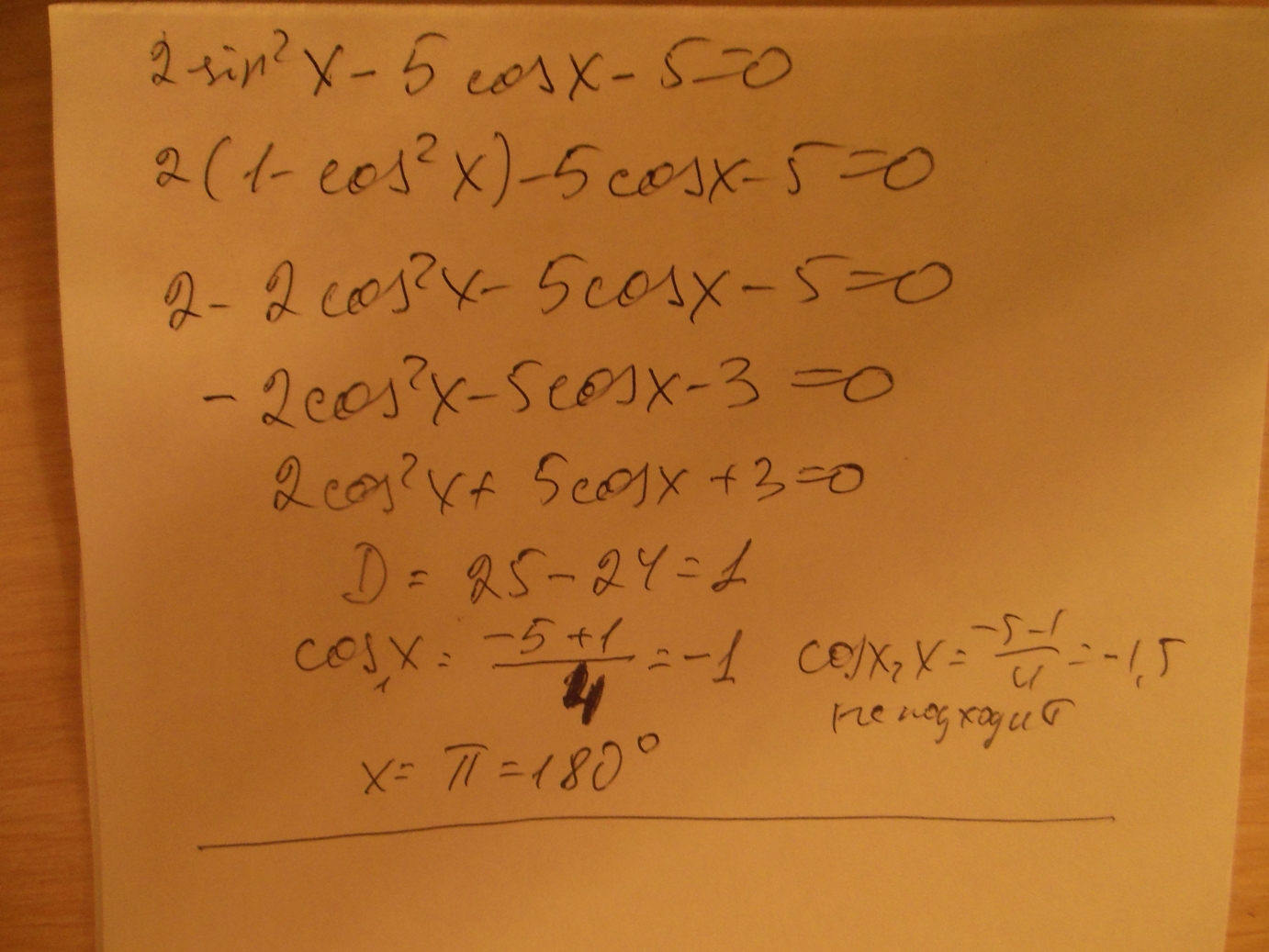
Похожие вопросы
Предмет: Математика,
автор: vanyadremka
Предмет: Математика,
автор: florezlive16
Предмет: Литература,
автор: dzintarsbogdanovs
Предмет: Биология,
автор: Аноним
Предмет: География,
автор: koroleva6969