Question

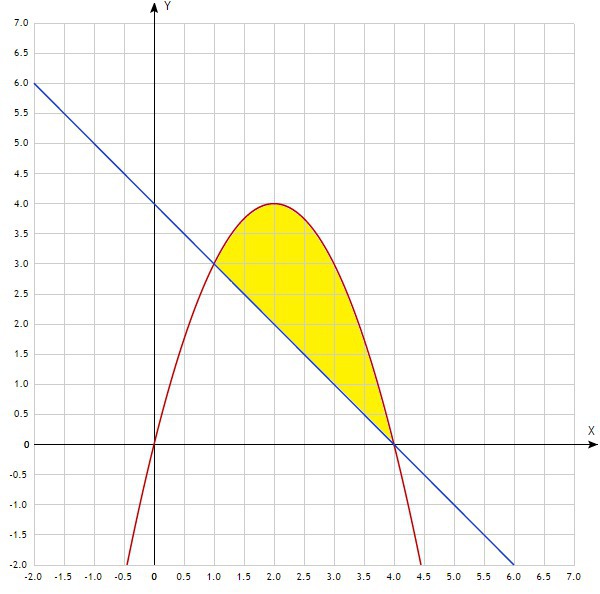
найти площадь фигуры ограниченной графиками функций y=4x-x^2 , y=4-x

Answer 1

Площадь фигуры, ограниченной графиками это определённый интеграл. Для нахождения пределов интегрирования необходимо построить чертёж или решить уравнение (но лучше сделать чертёж):
4x-x²=4-x
-x²+4x+x-4=0
-x²+5x-4=0
D=5²-4*(-1)*(-4)=25-16=9
x=(-5-3)/-2=4        x=(-5+3)/-2=1
Нашли нижний х=1 и верхний х=4 пределы.
На отрезке [1;4] график функции y=4x-x² лежит выше графика функции y=4-x, поэтому площадь фигуры
$S= intlimits^4_1 {((4x-x^2)-(4-x))} , dx= intlimits^4_1 {(-x^2+5x-4)} , dx =$
$=- frac{x^3}{3}+ frac{5x^2}{2}-4x|_1^4=- frac{4^3}{3}+ frac{5*4^2}{2}-4*4-(- frac{1}{3}+ frac{5*1}{2}-4*1)=$
$= frac{64}{3}+ frac{80}{2}-16+ frac{1}{3}- frac{5}{2}+4= 7- frac{5}{2} =4,5$ ед²