Предмет: Алгебра,
автор: Faler
Решить 1.27 методом интервалов
Приложения:
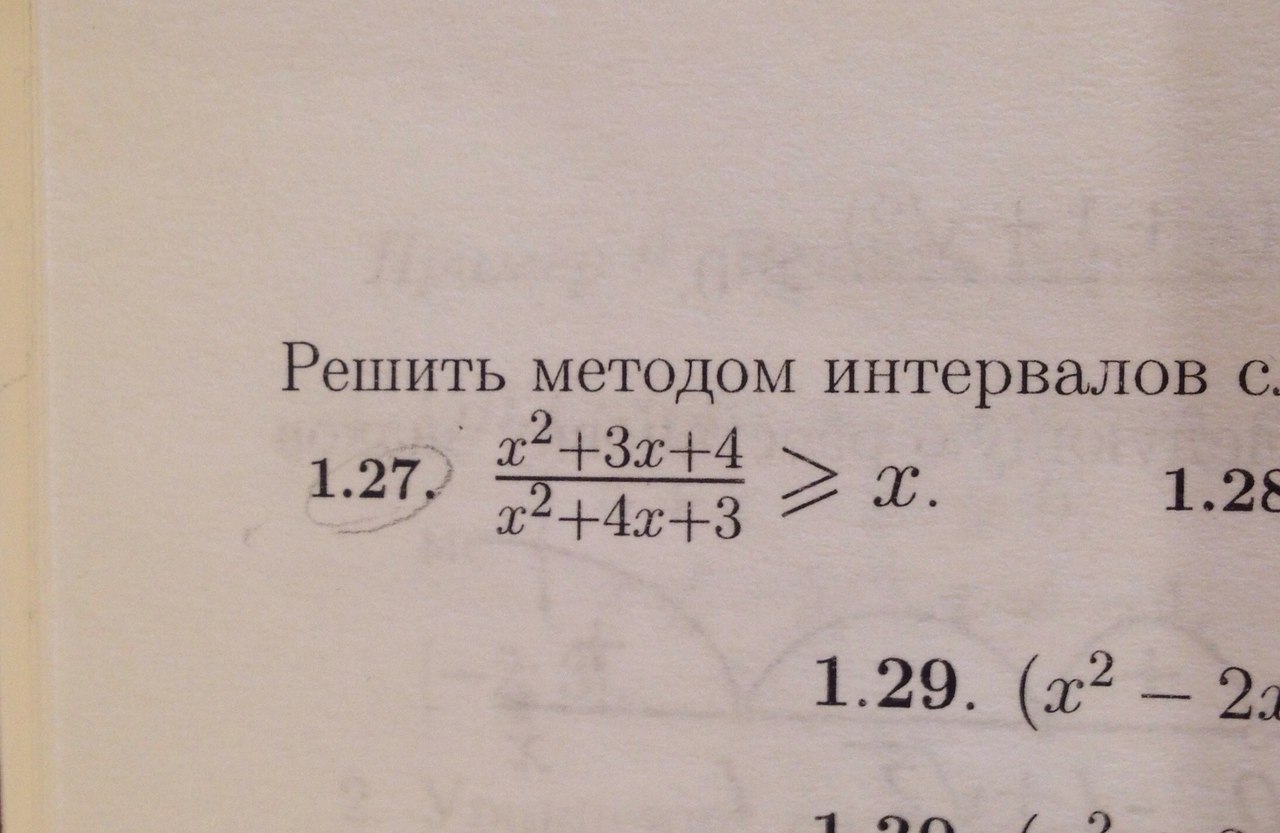
Ответы
Автор ответа:
0
Отметим все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов
________-3_____-2_____-1___________1_____>x
Вычислим знак (плюс или минус) функции на каждому интервале. Для этого достаточно подставить в f (x) любое число, которое будет правее всех отмеченных корней.
_____+___-3__ -___-2___-__-1_____+______1__-___>x
x∈(-∞; -3)∪(-1; +1]∪{-2}
Похожие вопросы
Предмет: Другие предметы,
автор: Liza3584567
Предмет: Химия,
автор: kate4534
Предмет: Алгебра,
автор: star12122008st
Предмет: Математика,
автор: etrio
Предмет: Физика,
автор: ilona11252001