Предмет: Математика,
автор: nastasyatrapez
найти производную: cos(x/y)+3^(4y)=0
Ответы
Автор ответа:
0
Обозначим 
Производную находим по формуле



Производную находим по формуле
Автор ответа:
0
В последнем выражении не нужен минус.
Автор ответа:
0
точно, опечатка!
Автор ответа:
0
смотрите решение фото
Приложения:
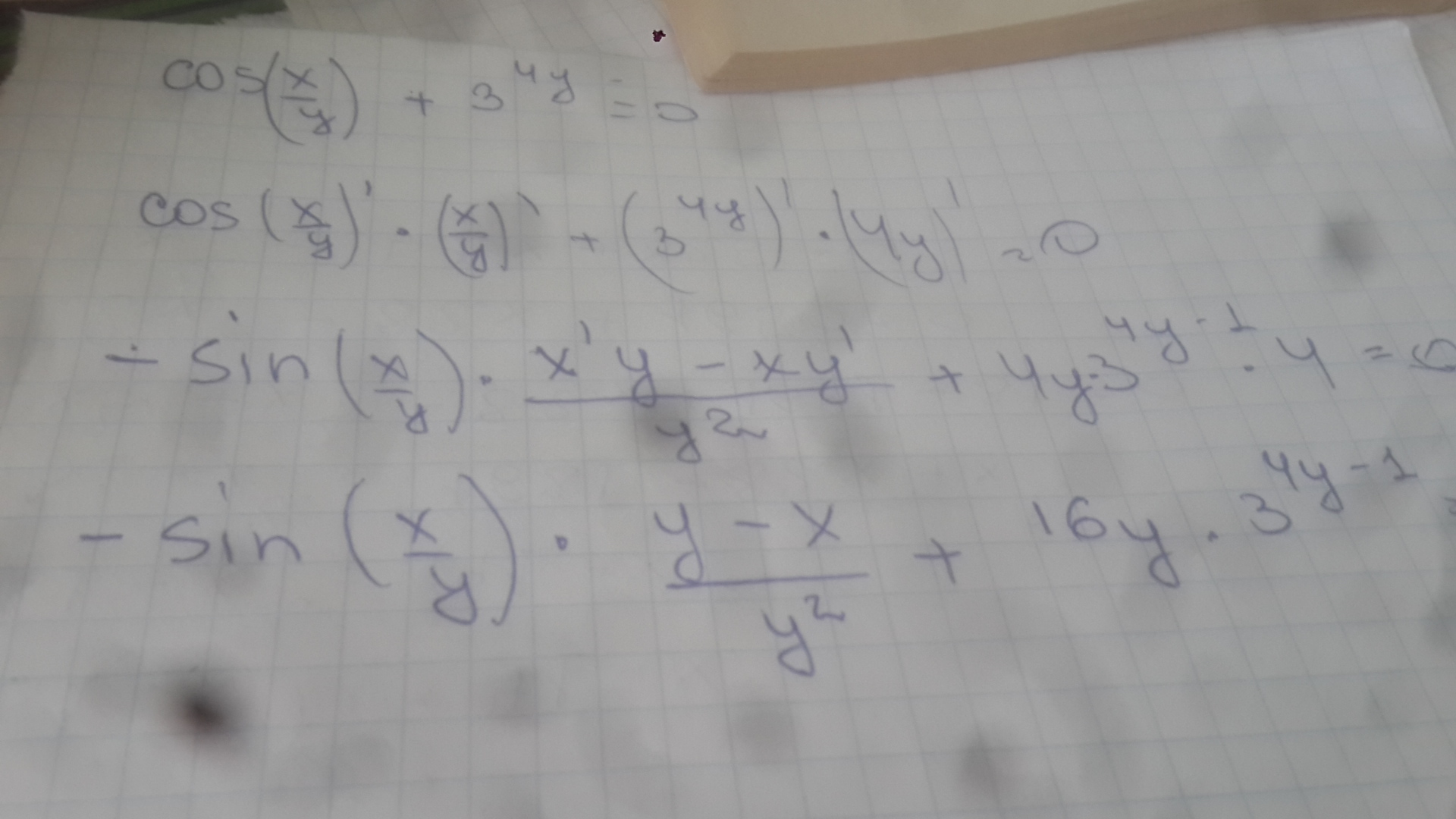
Похожие вопросы
Предмет: Математика,
автор: Dmima
Предмет: Окружающий мир,
автор: sevamalov
Предмет: Литература,
автор: kusana099
Предмет: Информатика,
автор: prihodkokp