Question

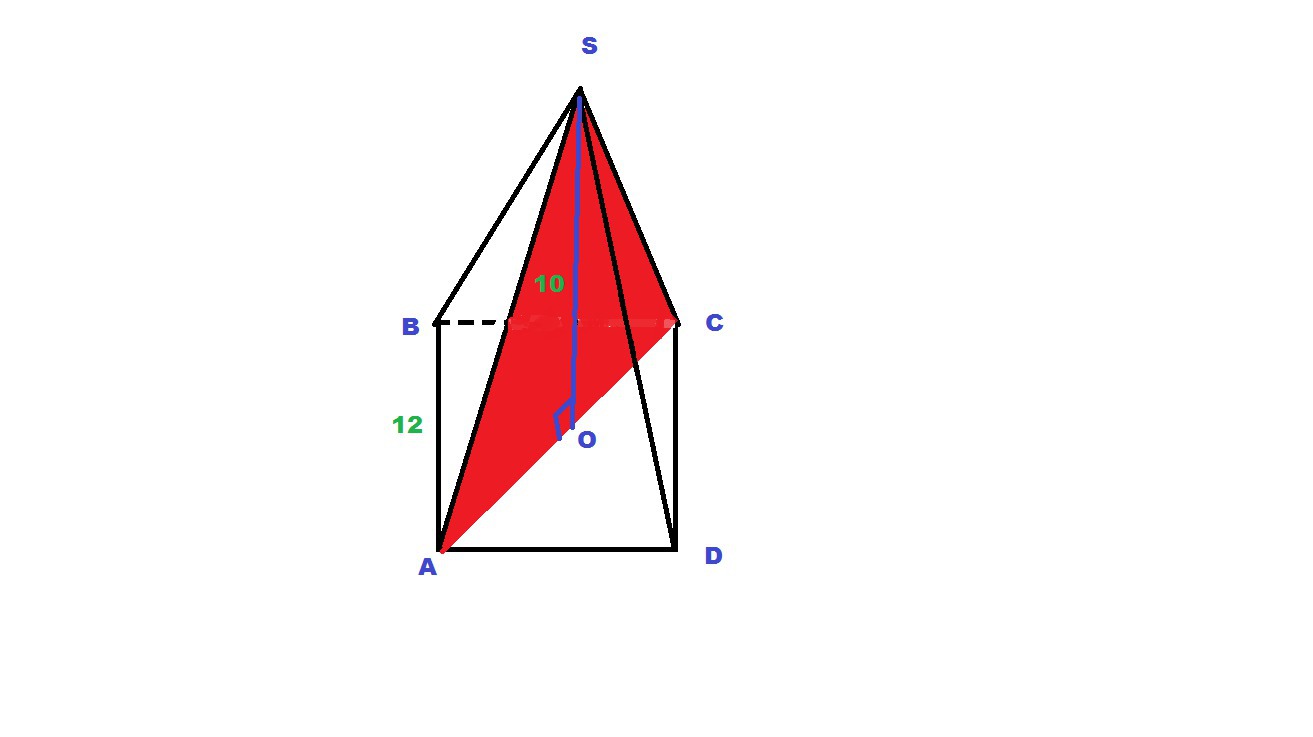
высота правильной четырехугольной пирамиды SABCD равна 10. сторона основания 12. найдите площадь диогонального сечения

Answer 1

Дано:

SABCD - правильная четырехугольная пирамида
SO - высота = 10
АВ - сторона основания = 12
_____________________
Найти:
Площадь диагонального сечения

Решение:

SABCD - правильная пирамида, в основании которой лежит квадрат.

Диагональное сечение представляет собой равнобедренный треугольник SAC

Площадь равнобедренного треугольника находится по формуле 
(произведение половины основания треугольника на его высоту):

$S_{triangle}= frac{SOcdot AC}{2}$
SO - высота
AC - основание равнобедренного треугольника ASC

Основанием нашего треугольника является диагональ квадрата ABCD, которую находим по теореме Пифагора:

$AC=sqrt{12^2cdot 2}=12sqrt2$

Тогда площадь равнобедренного треугольника ASC, которое и есть площадь сечения данной пирамиды, будет равно:


$S_{triangle}=frac{SOcdot AC}{2}\\ S_{triangle} = frac{10cdot12sqrt{2}}{2}=60sqrt2$

Ответ: $60sqrt{2}$ кв.ед.