Предмет: Математика,
автор: Alexsander091
Даю 30б! Помогите решить,распишите всё подробно пожалуйста))
Приложения:
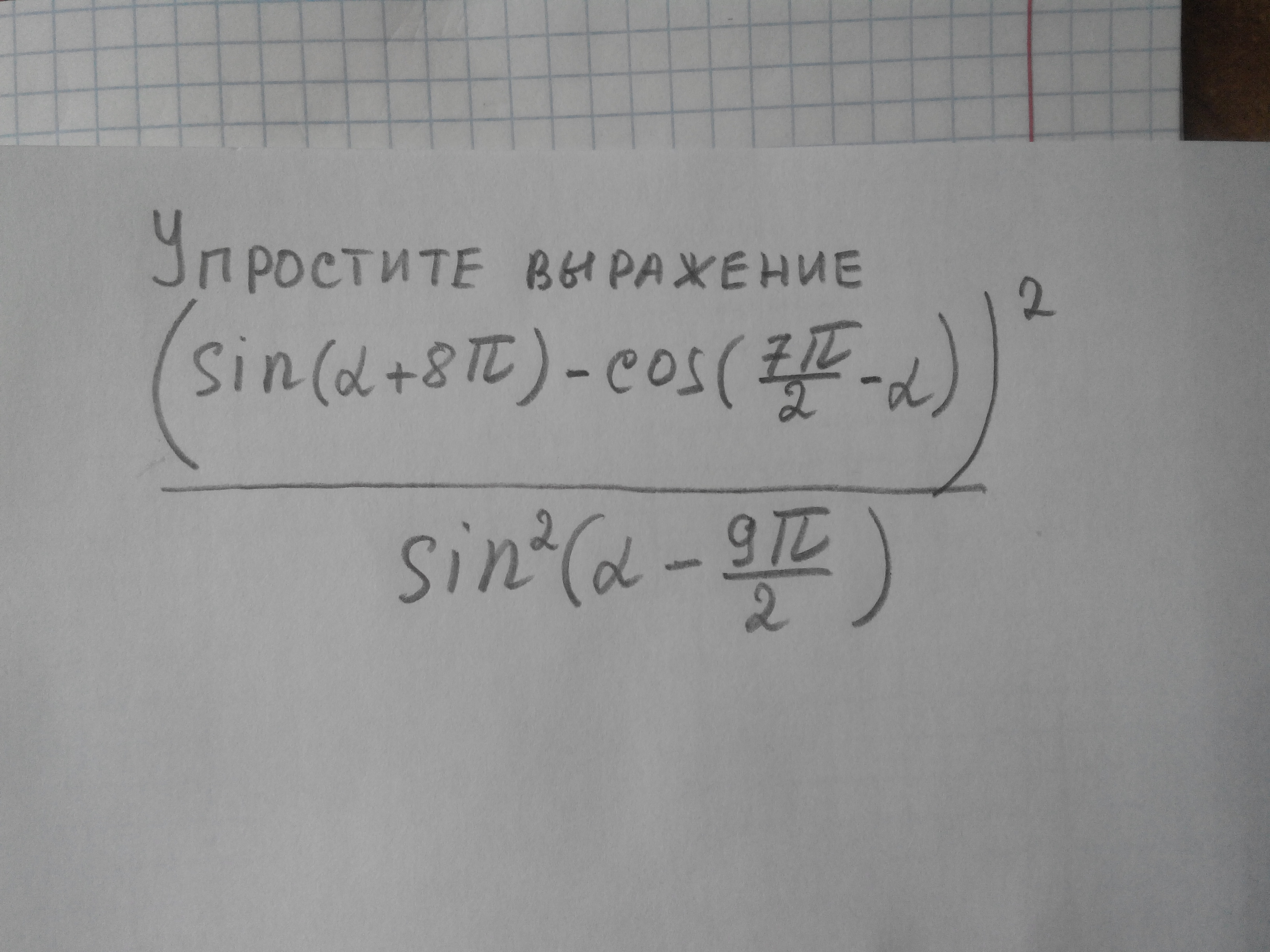
Ответы
Автор ответа:
0
(Sin[a+8 pi]-Cos[7 pi/2 -a])^2/(Sin[a-9 pi/2])^2= (Sin[a]-(-Sin[a]))^2/(Cos[a])^2 = 4 (Tan[a])^2
Все формулы, что потребовались- 2pi периодичность синуса и сумма аргументов синуса и косинуса
Sin[a+8 pi]= Sin[a]
Sin[a-9 pi/2]=Sin[a-pi/2]=Sin[a]*Cos[pi/2]-Cos[a]*Sin[pi/2]= -Cos[a]
Cos[7pi/2-a]= Cos[7pi/2]Cos[a]+Sin[7pi/2]Sin[a]=-Sin[a]
Остается только подставить
Все формулы, что потребовались- 2pi периодичность синуса и сумма аргументов синуса и косинуса
Sin[a+8 pi]= Sin[a]
Sin[a-9 pi/2]=Sin[a-pi/2]=Sin[a]*Cos[pi/2]-Cos[a]*Sin[pi/2]= -Cos[a]
Cos[7pi/2-a]= Cos[7pi/2]Cos[a]+Sin[7pi/2]Sin[a]=-Sin[a]
Остается только подставить
Автор ответа:
0
надо полностью решение!!!
Автор ответа:
0
Sin[a+8 pi]= Sin[a]
Sin[a-9 pi/2]=Sin[a-pi/2]=Sin[a]*Cos[pi/2]-Cos[a]*Sin[pi/2]= -Cos[a]
Cos[7pi/2-a]= Cos[7pi/2]Cos[a]+Sin[7pi/2]Sin[a]=-Sin[a]
Sin[a-9 pi/2]=Sin[a-pi/2]=Sin[a]*Cos[pi/2]-Cos[a]*Sin[pi/2]= -Cos[a]
Cos[7pi/2-a]= Cos[7pi/2]Cos[a]+Sin[7pi/2]Sin[a]=-Sin[a]
Автор ответа:
0
Имея такие замены, просто подставив их в начальное выражение, получим
Автор ответа:
0
(Sin[a]+Sin[a])^2/(-Cos[a])^2=4 (Tan[a])^2
Автор ответа:
0
Вот и все решение
Похожие вопросы
Предмет: Физика,
автор: zenioa21765hy
Предмет: Другие предметы,
автор: zuzapop20
Предмет: Физика,
автор: BoI7poC
Предмет: Математика,
автор: lasumka28
Предмет: Биология,
автор: ShayDee