Предмет: Алгебра,
автор: g2590757
Используя метод математической индукции, докажите, что при любом натуральном n
Приложения:
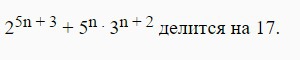
Ответы
Автор ответа:
0
1) проверяем справедливость при n=1.

верно.
2) предполагаем что утверждение верно для n, тогда оно будет верно и для (n+1). Проверяем.

1 слагаемое суммы делиться на 17, т.к. содержит такой множитель.
2 слагаемое суммы тоже делится на 17, т.к. выражение в скобках делится на 17(по нашему предположению).
Значит и сумма делится на 17.
Согласно методу мат. индукции это будет справедливо для любых натуральных n.
верно.
2) предполагаем что утверждение верно для n, тогда оно будет верно и для (n+1). Проверяем.
1 слагаемое суммы делиться на 17, т.к. содержит такой множитель.
2 слагаемое суммы тоже делится на 17, т.к. выражение в скобках делится на 17(по нашему предположению).
Значит и сумма делится на 17.
Согласно методу мат. индукции это будет справедливо для любых натуральных n.
Автор ответа:
0
==========================================>>>>+++
Приложения:

Похожие вопросы
Предмет: Литература,
автор: Gadel16
Предмет: Английский язык,
автор: nikataran08
Предмет: Математика,
автор: sdenisen815
Предмет: Литература,
автор: alihan120443
Предмет: Химия,
автор: dshvl