Question

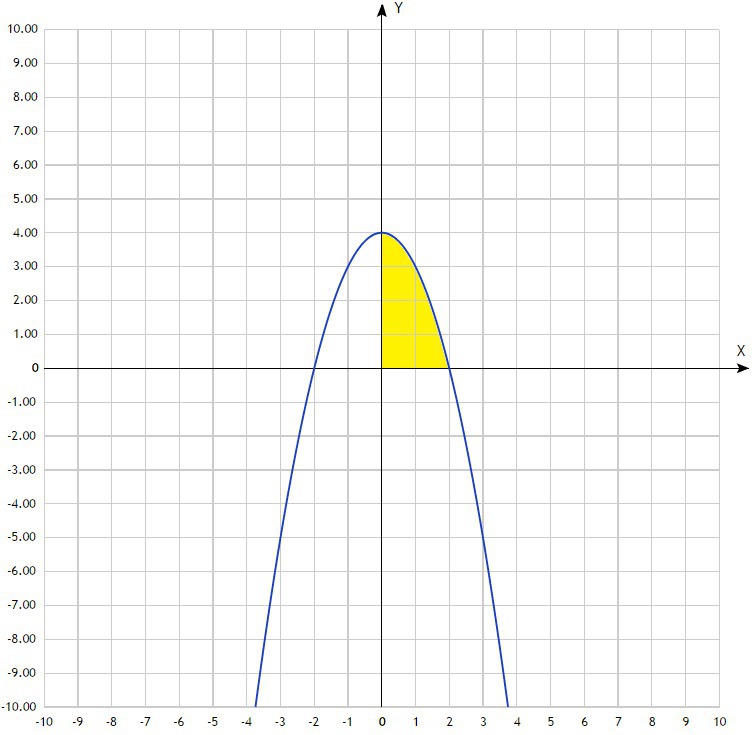
Найдите площадь фигуры, ограниченной заданными
линиями:
у=4-х(во второй степени)
У=0
Х=0
Х=2
Помогите!(

Answer 1

Площадь фигуры это определённый интеграл от функции, ограничивающей эту фигуру. Чертим чертёж (это обязательно). Учитываем, что у=0 это ось ОХ, а х=0 это ось ОY. Из чертежа сразу видно о какой фигуре идёт речь.
На отрезке [0;2] график функции y=4-x² расположен над осью ОХ, поэтому
$S= intlimits^2_0 {(4-x^2)} , dx=4x- frac{x^3}{3}|_{0}^{2}=4*2- frac{2^3}{3}=8- frac{8}{3}= frac{16}{3}=5 frac{1}{3}$ ед²