Предмет: Математика,
автор: LenkoV
Полное исследование функции и ее график
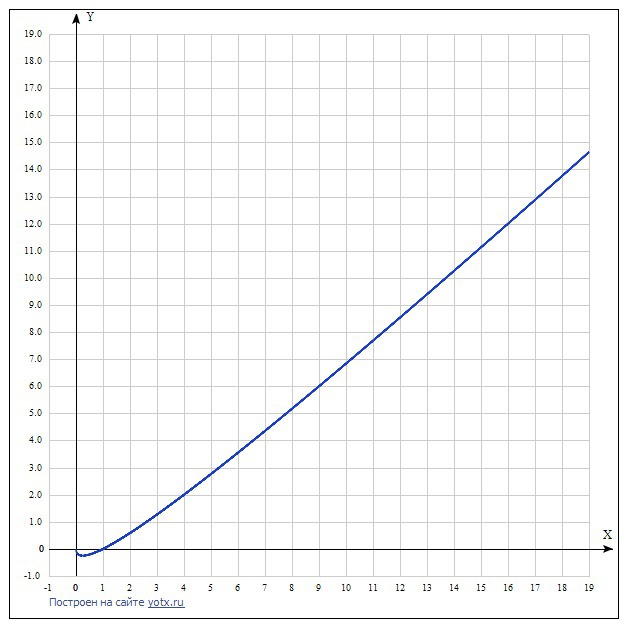
f(x)=x- корень из x
Ответы
Автор ответа:
0
Приложения:
Похожие вопросы
Предмет: Химия,
автор: romababenko2005
Предмет: Музыка,
автор: elenaignatyeva1
Предмет: Английский язык,
автор: superpapabatia
Предмет: Геометрия,
автор: Katerinalep
Предмет: Информатика,
автор: egoruchevaAlyo