Предмет: Математика,
автор: Ваня2142
как найти площадь фигуры ограниченной линиями y=1-x^2, осью Ox
Ответы
Автор ответа:
0
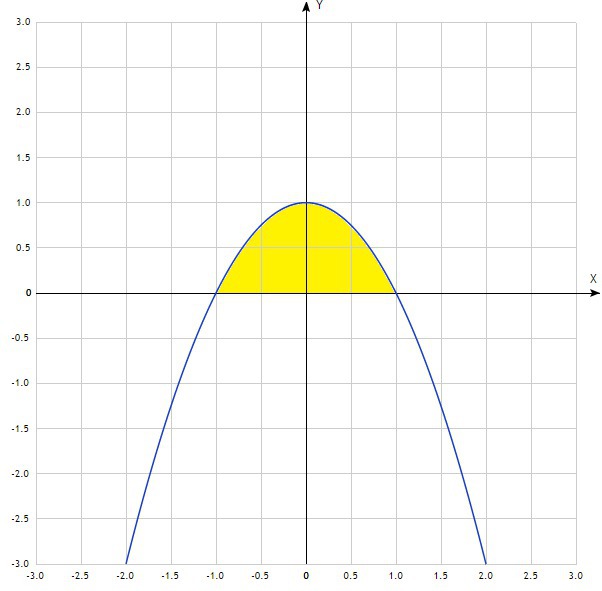
Для лучшего восприятия надо начертить график функции и тогда сразу будет видно о какой фигуре идёт речь. Чтобы найти площадь фигуры ограниченной линиями необходимо вычислить интеграл от функции ограничивающей эту фигуру. В нашем случае это парабола ветви которой направлены вниз. Нас интересует фигура, ограниченная параболой и осью ОХ. Определяем пределы интегрирования. Это можно сделать
по чертежу: это точки пересечения параболу с осью ОХ х=-1 и х=1
и аналитически, решив уравнение:
1-x²=0
-x²=-1
x²=1
x=1 x=-1
Далее находим площадь по формуле

 ед².
ед².
по чертежу: это точки пересечения параболу с осью ОХ х=-1 и х=1
и аналитически, решив уравнение:
1-x²=0
-x²=-1
x²=1
x=1 x=-1
Далее находим площадь по формуле
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: zoromarakagmailcom
Предмет: Алгебра,
автор: dakovt
Предмет: Математика,
автор: levitskijartem46
Предмет: Математика,
автор: Agward
Предмет: Литература,
автор: bisavka