Предмет: Математика,
автор: DMvel225
Исследовать на экстремум функции y=-x^3-4x^2+3x+8
Ответы
Автор ответа:
0
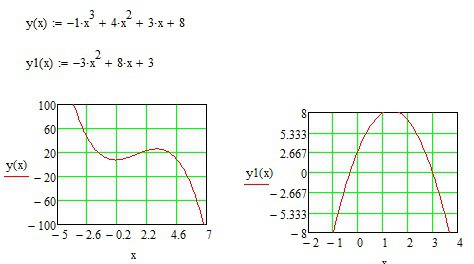
Точки экстремума - это точки, в которых производная y'(x) равна нулю. Уравнение производной y'(x)=-3*x²+8*x+3 - парабола. Равенство производной нулю определяем путём решения квадратного уравнения, в итоге находим координаты x1=-0,333 и x2=3. В точке x1 производная меняет знак с - на + и поэтому эта точка локального максимума, в точке x2 - c + на минус и поэтому это точка локального максимума. График функции и производной y1(x) показаны на рисунке.
Приложения:
Автор ответа:
0
Лучший!
Автор ответа:
0
Пишите, если будут проблемы
Автор ответа:
0
Найдём область определения функции: D(y) = R
Найдём производную функции: = 3х² - 4* 2х + 0 = 3х² - 8х
Область определения производной : R
Найдём нули производной: 3х² - 8х = 0
х * (3х - 8) = 0
1) х=0 2) 3х-8 =0
3х=8
х = 8/3
_____+____ 0 ______-________ 8/3_____+_____
↑ ↓ ↑
Итак, х =0 точка максимума, х = 8/3 - точка минимума функции.
Найдём производную функции: = 3х² - 4* 2х + 0 = 3х² - 8х
Область определения производной : R
Найдём нули производной: 3х² - 8х = 0
х * (3х - 8) = 0
1) х=0 2) 3х-8 =0
3х=8
х = 8/3
_____+____ 0 ______-________ 8/3_____+_____
↑ ↓ ↑
Итак, х =0 точка максимума, х = 8/3 - точка минимума функции.
Приложения:

Похожие вопросы
Предмет: Химия,
автор: mrroman900games
Предмет: Алгебра,
автор: olenatorino39
Предмет: Українська мова,
автор: galinacuk1107
Предмет: Математика,
автор: mmv777