Предмет: Алгебра,
автор: Animeshnikq
Вычислить предел( любой , желательно первый) . Решите пожалуйста , не могу решить, а скоро экзамен... ( задание в приложении
Приложения:
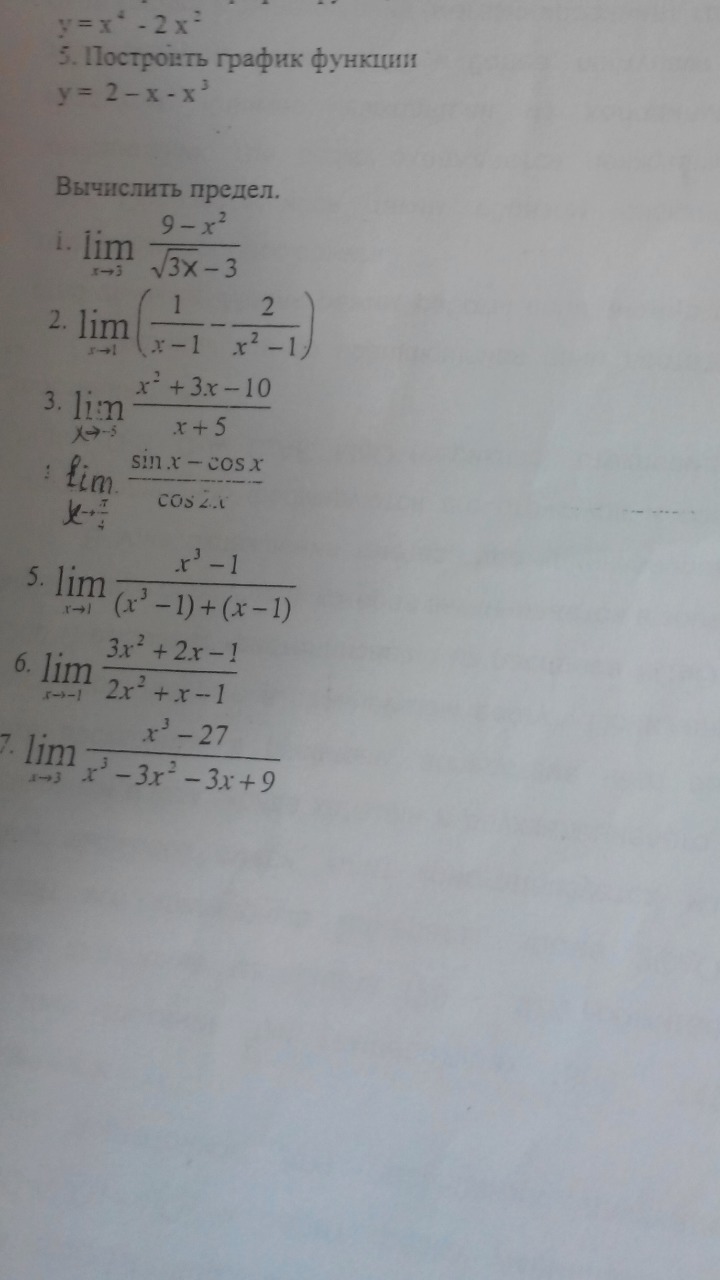
Ответы
Автор ответа:
0
1.

2.

3.
Разложим x²+3x-10 на множители:
x²+3x-10=0
D=9+40=49
x₁=(-3-7)/2= -5
x₂=(-3+7)/2=2
x²+3x-10=(x+5)(x-2)

4.

5.

6.
Разложим на множители:
3x²+2x-1=0
D=4+12=16
x₁=(-2-4)/6=-1
x₂=(-2+4)/6=2/6=1/3
3x²+2x-1=3(x+1)(x - ¹/₃) = (x+1)(3x-1)
Разложим на множители:
2x²+x-1=0
D=1+8=9
x₁=(-1-3)/4=-1
x₂=(-1+3)/4=2/4=1/2
2x²+x-1=2(x+1)(x-¹/₂)=(x+1)(2x-1)

7.

2.
3.
Разложим x²+3x-10 на множители:
x²+3x-10=0
D=9+40=49
x₁=(-3-7)/2= -5
x₂=(-3+7)/2=2
x²+3x-10=(x+5)(x-2)
4.
5.
6.
Разложим на множители:
3x²+2x-1=0
D=4+12=16
x₁=(-2-4)/6=-1
x₂=(-2+4)/6=2/6=1/3
3x²+2x-1=3(x+1)(x - ¹/₃) = (x+1)(3x-1)
Разложим на множители:
2x²+x-1=0
D=1+8=9
x₁=(-1-3)/4=-1
x₂=(-1+3)/4=2/4=1/2
2x²+x-1=2(x+1)(x-¹/₂)=(x+1)(2x-1)
7.
Похожие вопросы
Предмет: Литература,
автор: mrelizar4
Предмет: Українська мова,
автор: Аноним
Предмет: Математика,
автор: fsdkfksd
Предмет: География,
автор: Аноним
Предмет: Химия,
автор: Zakharova51