Предмет: Математика,
автор: любимица2
Помогите, пожалуйста,решить ;)
Приложения:
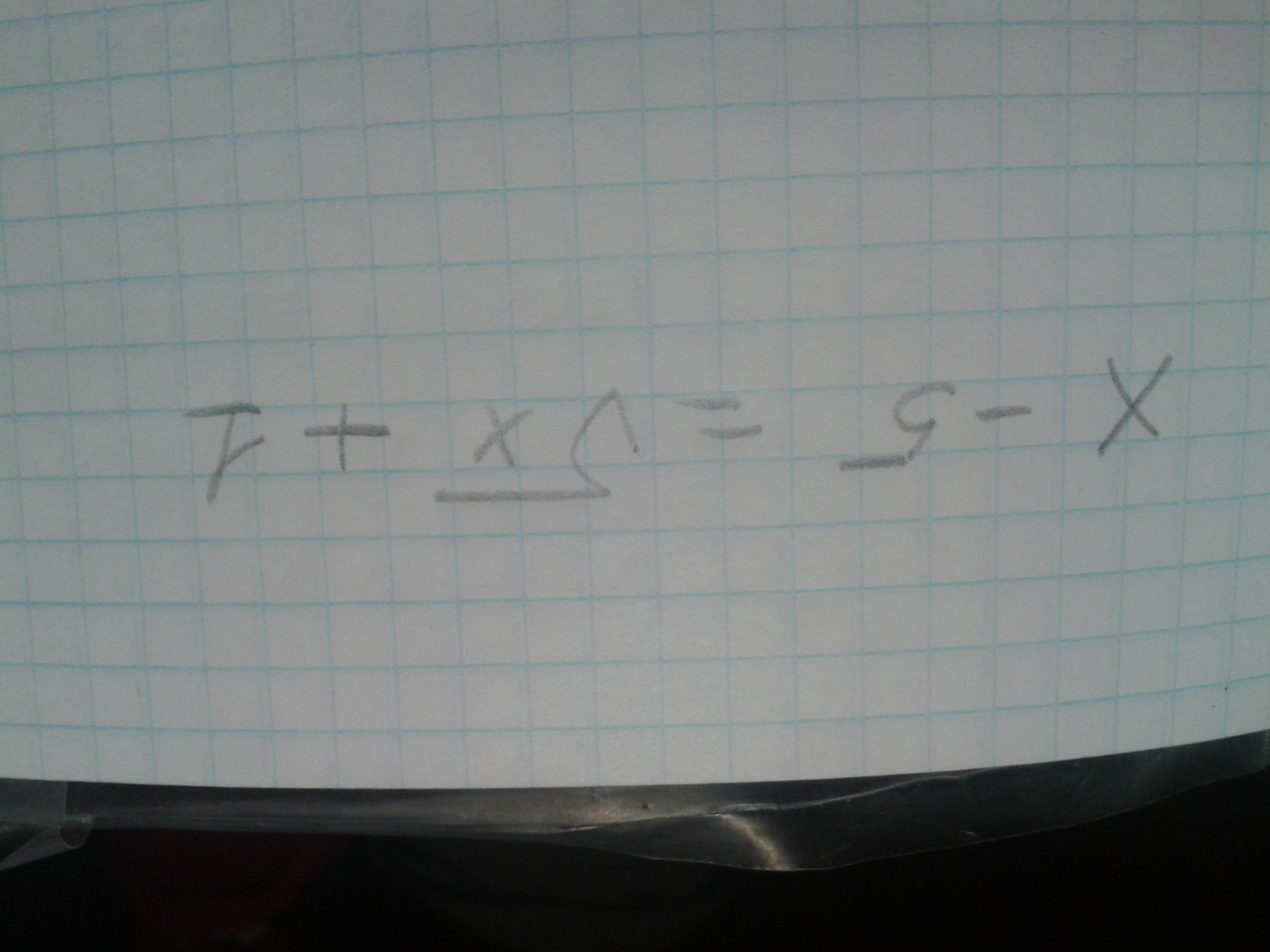
Ответы
Автор ответа:
0
х-5=√х +1
х-5-1=√х
(х-6)²=(√х)²
х²-12х+36=х
х²-12х-х+36=0
x²-13x+36=0
D=(-13)²-4*1*36=169-144=25
x₁=(13+5)2=182=9
x₂=(13-5)2=82=4
Проверяем корни:
1) 9-5=√9 +1
4=3+1
4=4
Корень подходит.
Теперь проверяем второй корень:
2) 4-5=√4+1
-1=2+1
-1≠3
Корень 4 не подходит)
Ответ: 9
х-5-1=√х
(х-6)²=(√х)²
х²-12х+36=х
х²-12х-х+36=0
x²-13x+36=0
D=(-13)²-4*1*36=169-144=25
x₁=(13+5)2=182=9
x₂=(13-5)2=82=4
Проверяем корни:
1) 9-5=√9 +1
4=3+1
4=4
Корень подходит.
Теперь проверяем второй корень:
2) 4-5=√4+1
-1=2+1
-1≠3
Корень 4 не подходит)
Ответ: 9
Автор ответа:
0
Дано уравнение: х - 5 = √х + 1.
Перенесём 1 влево: √х = х - 6.
Так как подкоренное выражение не может быть отрицательным, то определяем ОДЗ: х - 6 ≥ 0 или х ≥ 6.
Возведём обе части -выражения √х = х - 6 в квадрат:
х = х² - 12х + 36.
Получаем квадратное уравнение:
х² - 13х + 36 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=(-13)^2-4*1*36=169-4*36=169-144=25;
Дискриминант больше 0, уравнение имеет 2 корня:x₁=(√25-(-13))/(2*1)=(5-(-13))/2=(5+13)/2=18/2=9;x₂=(-√25-(-13))/(2*1)=(-5-(-13))/2=(-5+13)/2=8/2=4.
Второй корень отбрасываем по ОДЗ.
Ответ: х = 9.
Перенесём 1 влево: √х = х - 6.
Так как подкоренное выражение не может быть отрицательным, то определяем ОДЗ: х - 6 ≥ 0 или х ≥ 6.
Возведём обе части -выражения √х = х - 6 в квадрат:
х = х² - 12х + 36.
Получаем квадратное уравнение:
х² - 13х + 36 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=(-13)^2-4*1*36=169-4*36=169-144=25;
Дискриминант больше 0, уравнение имеет 2 корня:x₁=(√25-(-13))/(2*1)=(5-(-13))/2=(5+13)/2=18/2=9;x₂=(-√25-(-13))/(2*1)=(-5-(-13))/2=(-5+13)/2=8/2=4.
Второй корень отбрасываем по ОДЗ.
Ответ: х = 9.
Похожие вопросы
Предмет: Алгебра,
автор: hikoraduba
Предмет: Математика,
автор: ltimoschuk15
Предмет: Математика,
автор: ju6cny2y
Предмет: Алгебра,
автор: chinenkovairina
Предмет: Математика,
автор: Аноним