Предмет: Алгебра,
автор: denic190499
решить систему. подробно, если можно пояснить
Приложения:
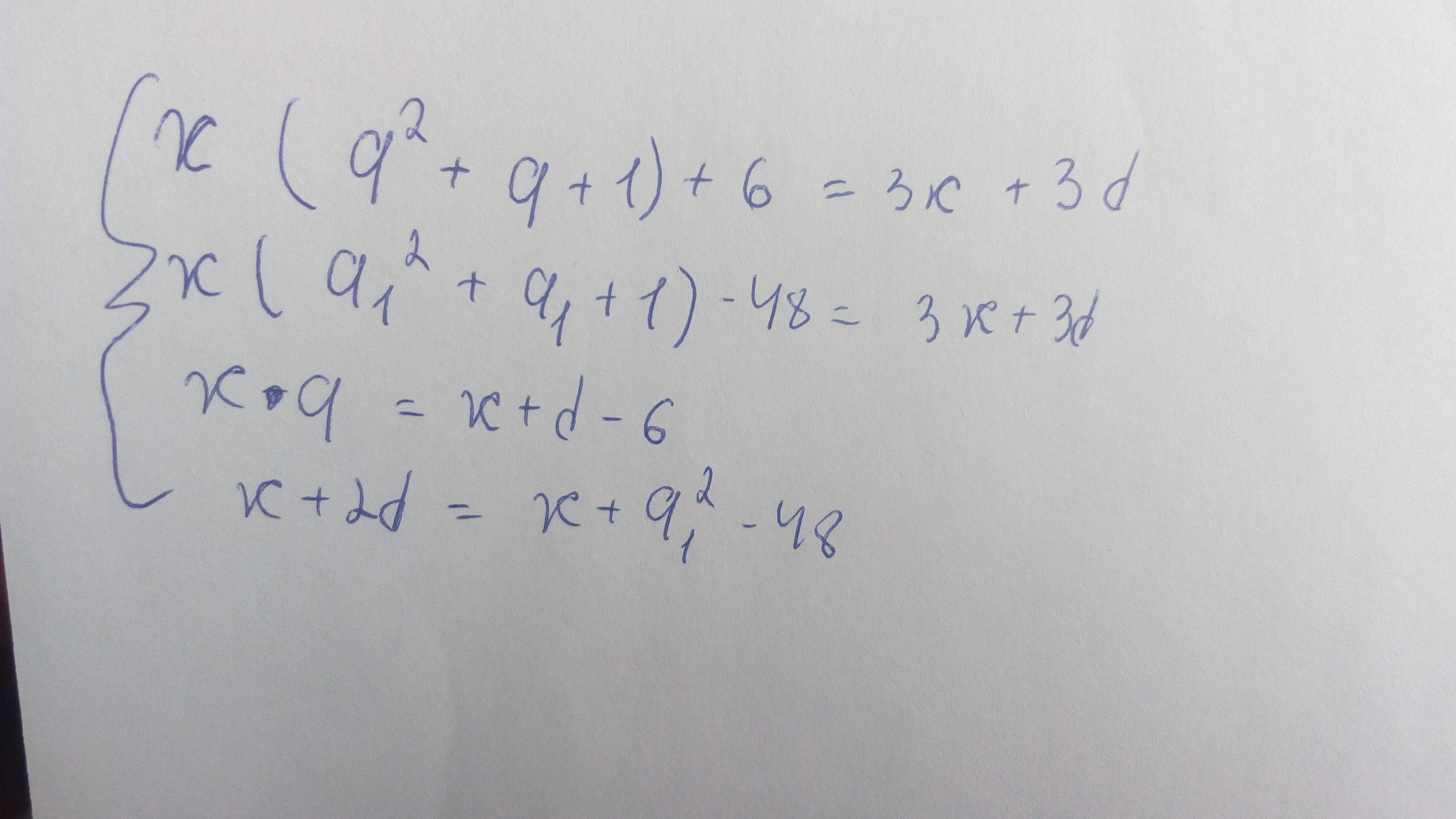
Ответы
Автор ответа:
0
Попробую, хотя система не простая
{ x(q^2 + q + 1) + 6 = 3x + 3d
{ x(a^2 + a + 1) - 48 = 3x + 3d
{ x*q = x + d - 6
{ x + 2d = x + a^2 - 48
В 4 уравнении можно вычесть x
2d = a^2 - 48
d = a^2/2 - 24
Подставляем
{ x(q^2 + q + 1) + 6 = 3x + 3(a^2/2 - 24)
{ x(a^2 + a + 1) - 48 = 3x + 3(a^2/2 - 24)
{ x*q = x - 6 + a^2/2 - 24
Упрощаем
{ x(q^2 + q + 1 - 3) = 1,5a^2 - 72 - 6 = 1,5a^2 - 78 = 1,5*(a^2 - 52)
{ x(a^2 + a + 1 - 3) = 1,5a^2 - 72 + 48 = 1,5a^2 - 24 = 1,5*(a^2 - 16)
{ x*(q - 1) = 0,5a^2 - 30
Из 2 уравнения
x = 1,5*(a^2 - 16) / (a^2 + a - 2) = 1,5(a^2 - 16) / (a^2 + a - 2)
Из 3 уравнения
q - 1 = 0,5(a^2 - 60) / x = 0,5(a^2 - 60)(a^2 + a - 2) / [1,5(a^2 - 16)]
q = 1 + (a^2 - 60)(a^2 + a - 2) / [3(a^2 - 16)] =
= [3(a^2 - 16) + (a^2 - 60)(a^2 + a - 2)] / [3(a^2 - 16)]
Из 1 и 2 уравнения
x = 1,5*(a^2 - 52) / [(q+2)(q-1)] = 1,5(a^2 - 16) / (a^2 + a - 2)
Получаем
(a^2 - 52)*(a^2 + a - 2) = (a^2 - 16)*(q+2)(q-1)
Подставляем q - 1
(a^2 - 52)*(a^2 + a - 2) = (a^2 - 16)*(q+2)(a^2 - 60)(a^2 + a - 2)/[3(a^2 - 16)]
Сокращаем
a^2 - 52 = (q + 2)(a^2 - 60)/3
q + 2 = 3(a^2 - 52)/(a^2 - 60)
q = [3(a^2-52) - 2(a^2-60)] / (a^2-60) = (a^2-156+120) / (a^2-60) = (a^2-36) / (a^2-60)
q = (a^2-36) / (a^2-60) = (a^2-60+24) / (a^2-60) = 1 + 24 / (a^2-60)
Приравниваем q
1 + (a^2 - 60)(a^2 + a - 2) / [3(a^2 - 16)] = 1 + 24 / (a^2 - 60)
(a^2 - 60)(a^2 + a - 2) / [3(a^2 - 16)] = 24 / (a^2 - 60)
(a^2 - 60)^2*(a^2 + a - 2) = 72(a^2 - 16)
Я не знаю, как это решать, помог Вольфрам Альфа.
Получается уравнение 6 степени, которое школьник решить не сможет.
a^6 + a^5 - 122a^4 - 120a^3 + 3768a^2 + 3600a - 6048 = 0
Оно имеет 6 иррациональных корней
a1 ~ -8,25; a2 ~ -7,226; a3 ~ -1,903; a4 ~ 0,892; a5 ~ 7,296; a6 ~ 8, 191
{ x(q^2 + q + 1) + 6 = 3x + 3d
{ x(a^2 + a + 1) - 48 = 3x + 3d
{ x*q = x + d - 6
{ x + 2d = x + a^2 - 48
В 4 уравнении можно вычесть x
2d = a^2 - 48
d = a^2/2 - 24
Подставляем
{ x(q^2 + q + 1) + 6 = 3x + 3(a^2/2 - 24)
{ x(a^2 + a + 1) - 48 = 3x + 3(a^2/2 - 24)
{ x*q = x - 6 + a^2/2 - 24
Упрощаем
{ x(q^2 + q + 1 - 3) = 1,5a^2 - 72 - 6 = 1,5a^2 - 78 = 1,5*(a^2 - 52)
{ x(a^2 + a + 1 - 3) = 1,5a^2 - 72 + 48 = 1,5a^2 - 24 = 1,5*(a^2 - 16)
{ x*(q - 1) = 0,5a^2 - 30
Из 2 уравнения
x = 1,5*(a^2 - 16) / (a^2 + a - 2) = 1,5(a^2 - 16) / (a^2 + a - 2)
Из 3 уравнения
q - 1 = 0,5(a^2 - 60) / x = 0,5(a^2 - 60)(a^2 + a - 2) / [1,5(a^2 - 16)]
q = 1 + (a^2 - 60)(a^2 + a - 2) / [3(a^2 - 16)] =
= [3(a^2 - 16) + (a^2 - 60)(a^2 + a - 2)] / [3(a^2 - 16)]
Из 1 и 2 уравнения
x = 1,5*(a^2 - 52) / [(q+2)(q-1)] = 1,5(a^2 - 16) / (a^2 + a - 2)
Получаем
(a^2 - 52)*(a^2 + a - 2) = (a^2 - 16)*(q+2)(q-1)
Подставляем q - 1
(a^2 - 52)*(a^2 + a - 2) = (a^2 - 16)*(q+2)(a^2 - 60)(a^2 + a - 2)/[3(a^2 - 16)]
Сокращаем
a^2 - 52 = (q + 2)(a^2 - 60)/3
q + 2 = 3(a^2 - 52)/(a^2 - 60)
q = [3(a^2-52) - 2(a^2-60)] / (a^2-60) = (a^2-156+120) / (a^2-60) = (a^2-36) / (a^2-60)
q = (a^2-36) / (a^2-60) = (a^2-60+24) / (a^2-60) = 1 + 24 / (a^2-60)
Приравниваем q
1 + (a^2 - 60)(a^2 + a - 2) / [3(a^2 - 16)] = 1 + 24 / (a^2 - 60)
(a^2 - 60)(a^2 + a - 2) / [3(a^2 - 16)] = 24 / (a^2 - 60)
(a^2 - 60)^2*(a^2 + a - 2) = 72(a^2 - 16)
Я не знаю, как это решать, помог Вольфрам Альфа.
Получается уравнение 6 степени, которое школьник решить не сможет.
a^6 + a^5 - 122a^4 - 120a^3 + 3768a^2 + 3600a - 6048 = 0
Оно имеет 6 иррациональных корней
a1 ~ -8,25; a2 ~ -7,226; a3 ~ -1,903; a4 ~ 0,892; a5 ~ 7,296; a6 ~ 8, 191
Похожие вопросы
Предмет: Алгебра,
автор: MonochromeButterfly
Предмет: Алгебра,
автор: pticinainna80
Предмет: Математика,
автор: artiommunteanu30
Предмет: Математика,
автор: nata306
Предмет: Биология,
автор: saran4ik