Предмет: Математика,
автор: dbnfkbr0079
Найти площадь фигуры ограниченной линиями.
1)y=x^2+3x и осью Ох
Ответы
Автор ответа:
0
y=x²+3x
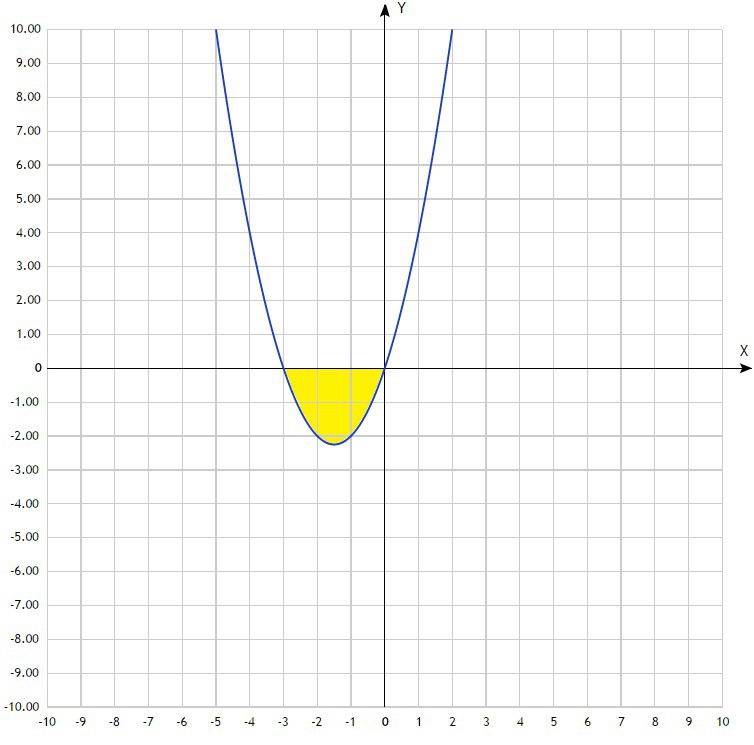
Лучше начать с построения чертежа, тогда легче понять о какой фигуре идёт речь. В нашем случае это парабола, ветви которой направлены вверх. Необходимо найти площадь фигуры, которая расположена ниже оси ОХ (см. чертёж во вложении) на отрезке [-3;0]. Вообще точки пересечения параболы и оси ОХ можно найти аналитически, т.е. решить уравнение
x²+3x=0
x(x+3)=0
x=0 x=-3
Значит нижний предел интегрирования а=-3, а верхний предел интегрирования b=-3
Так как фигура расположена под осью ОХ, её площадь определяется по формуле

 ед².
ед².
Ответ: S=4,5 ед²
Лучше начать с построения чертежа, тогда легче понять о какой фигуре идёт речь. В нашем случае это парабола, ветви которой направлены вверх. Необходимо найти площадь фигуры, которая расположена ниже оси ОХ (см. чертёж во вложении) на отрезке [-3;0]. Вообще точки пересечения параболы и оси ОХ можно найти аналитически, т.е. решить уравнение
x²+3x=0
x(x+3)=0
x=0 x=-3
Значит нижний предел интегрирования а=-3, а верхний предел интегрирования b=-3
Так как фигура расположена под осью ОХ, её площадь определяется по формуле
Ответ: S=4,5 ед²
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: Ivanka535
Предмет: Обществознание,
автор: KirillOBWAGA
Предмет: Математика,
автор: kuhtamasha8
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: lussy1982