Question

Найти площадь фигуры ограниченной линиями.
1)y=4-x^2 и y=x+2

Answer 1

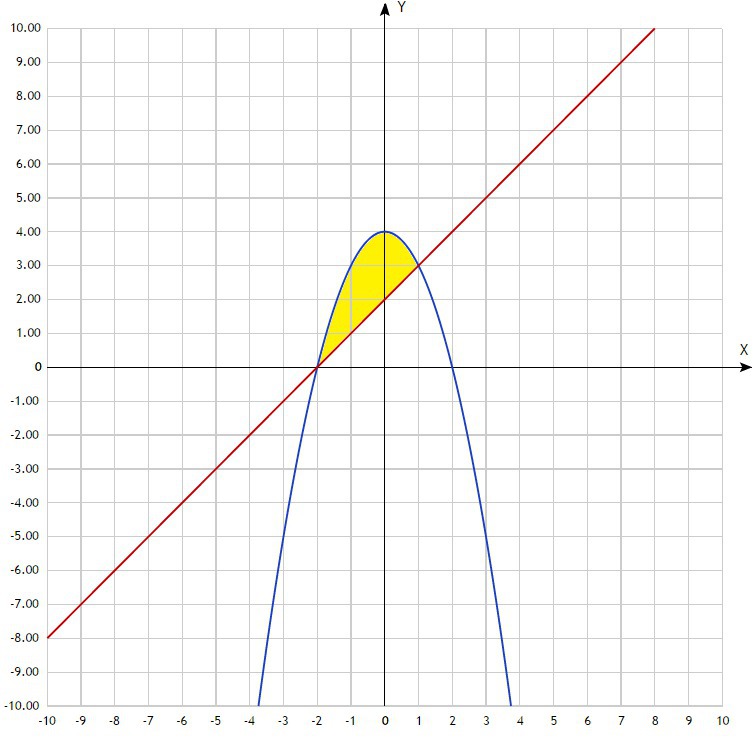
Для начала начертим чертёж и определим по нему точки пересечения линий. Вообще их можно найти и аналитически, решив уравнение
4-x²=x+2
-x²-x+2=0
D=(-1)²-4*(-1)*2=9
x=(1-3)/-2=1   x=(1+3)/-2=-2
Значит нижний предел интегрирования а=-2, верхний предел интегрирования b=1.
Если на отрезке [a;b] некоторая непрерывная функция f(x) больше либо равна некоторой непрерывной функции g(x), то площадь фигуры, ограниченной графиками данных функций можно найти по формуле
$S= intlimits^b_a {(f(x)-g(x))} , dx$
4-x²>x+2
Находим площадь
$S= intlimits^1_{-2} {(4-x^2-(x+2))} , dx = intlimits^1_{-2} {(2-x^2-x)} , dx =(2x- frac{x^3}{3}- frac{x^2}{2}) |_{-2}^{1}$
$=2*1- frac{1^3}{3}- frac{1^2}{2} -(2*(-2)- frac{(-2)^3}{3} - frac{(-2)^2}{2)} =$
$=2- frac{1}{3}- frac{1}{2}+4- frac{8}{3}+2=8-3- frac{1}{2}=4,5$ ед²

Ответ: S=4,5 ед²