Предмет: Геометрия,
автор: alivegrenade
Диагонали трапеции равны 10 и 24, а основания равны 7 и 19. Найдите угол между прямыми, содержащими диагонали трапеции.
Ответы
Автор ответа:
0
нормальная задачка.
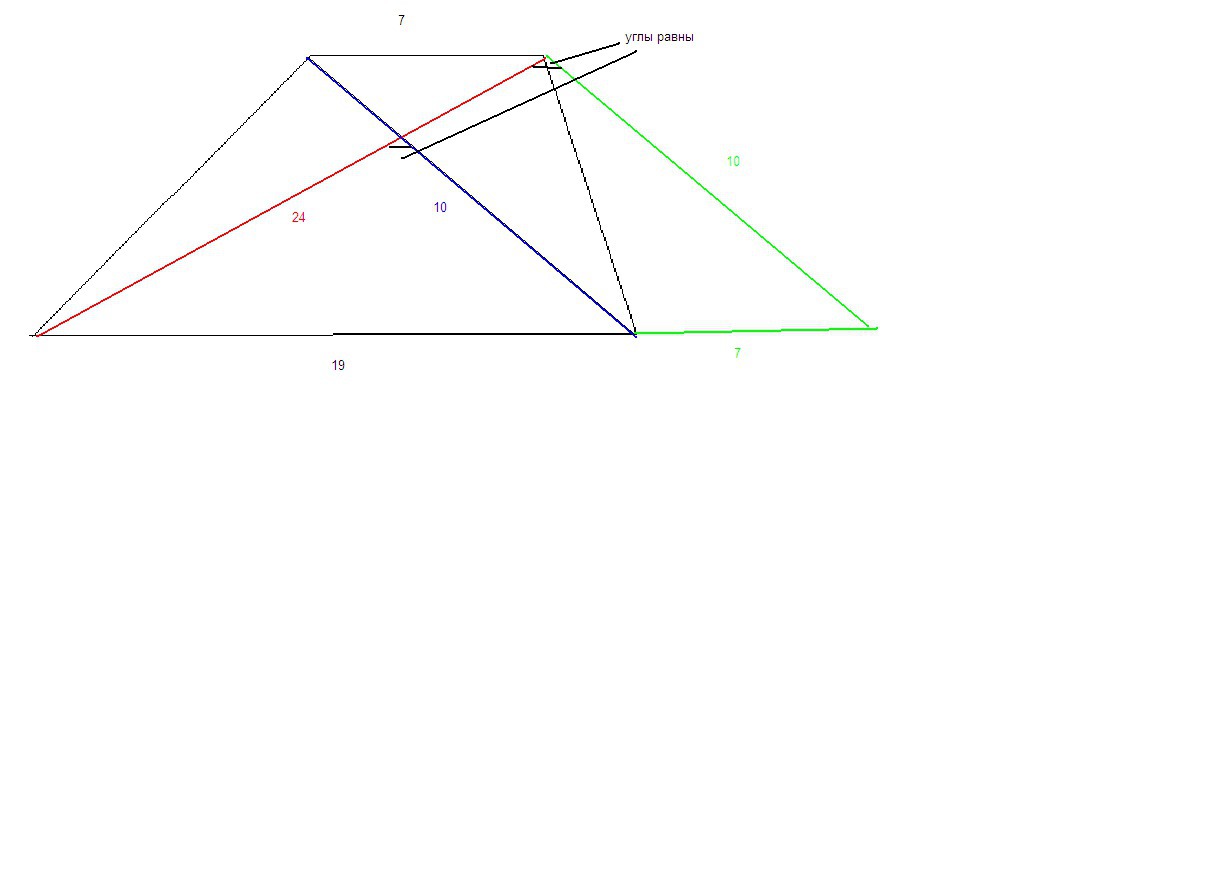
Для простоты решения сделаем допостроение, как на рисунке в файле.
теперь по теореме косинусов находим
(19+7)²=24²+10²-2*24*10*cos(α)
2*24*10*cos(α)=576+100-676=0
cos(α)=0 ⇒ α=90
если вы не учили еще либо не знаете теорему косинусов, то просто проверим, а не будет ли квадрат 24 плюс квадрат 10 равен квадрату 26?
24²+10²=576+100=676
26²=676
Ура! значит, согласно т.Пифагора, треугольник прямоугольный. Угол=90
Для простоты решения сделаем допостроение, как на рисунке в файле.
теперь по теореме косинусов находим
(19+7)²=24²+10²-2*24*10*cos(α)
2*24*10*cos(α)=576+100-676=0
cos(α)=0 ⇒ α=90
если вы не учили еще либо не знаете теорему косинусов, то просто проверим, а не будет ли квадрат 24 плюс квадрат 10 равен квадрату 26?
24²+10²=576+100=676
26²=676
Ура! значит, согласно т.Пифагора, треугольник прямоугольный. Угол=90
Приложения:
Автор ответа:
0
Спасибо большое, да ещё так быстро)
Автор ответа:
0
правда, мы ещё не проходили теорему косинусов
Автор ответа:
0
тогда 2-е решение
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: popka5146
Предмет: Биология,
автор: asemasatybaeva
Предмет: Математика,
автор: Angeloki
Предмет: Химия,
автор: Leoneedykt