Предмет: Математика,
автор: AlexanderBus
Решите неравенство написанное на рисунке
Приложения:
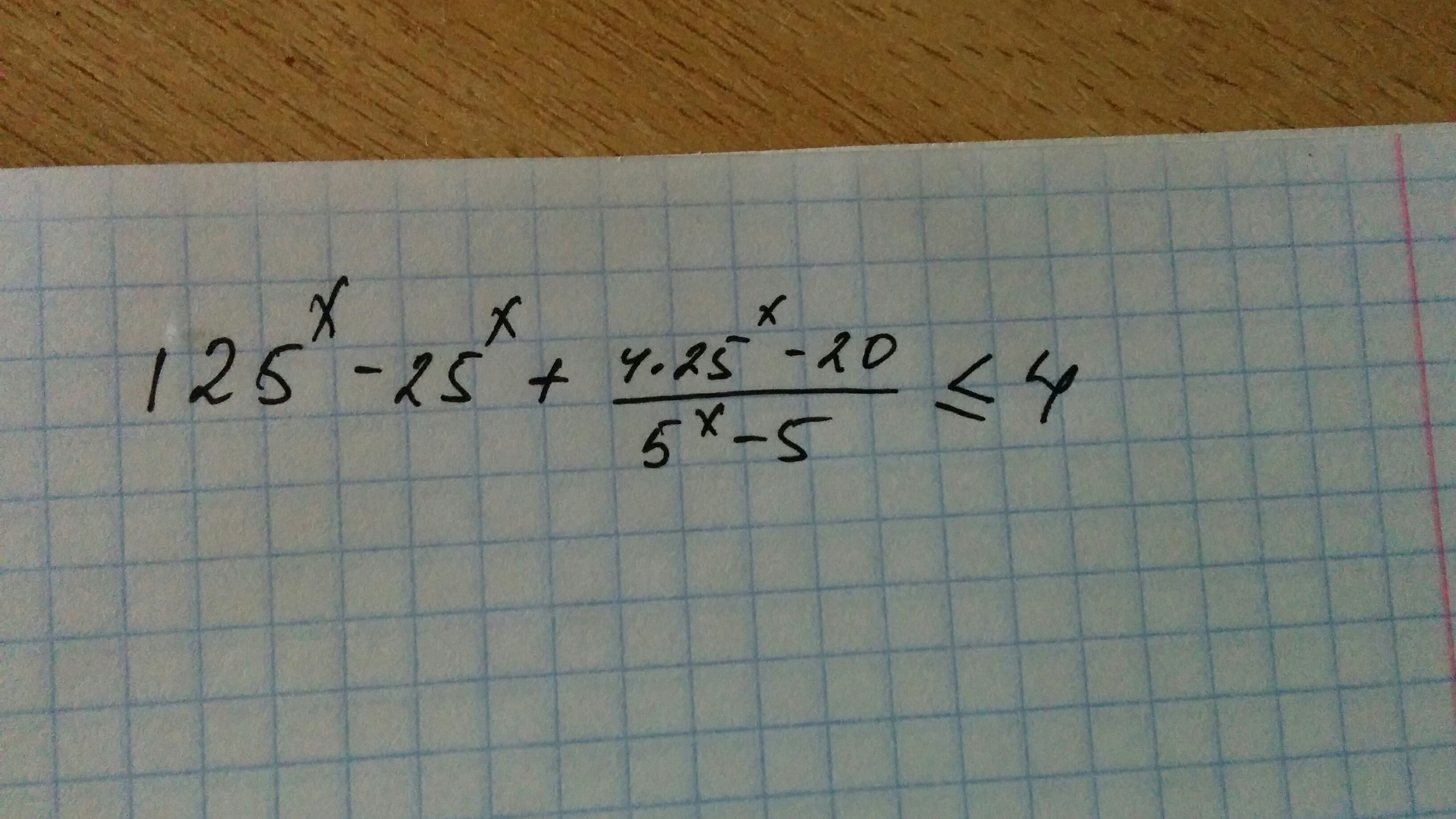
Ответы
Автор ответа:
0
Замена 5^x=t, t>0

Получаем, что методом интервалов решением будут t∈[4;5)U{1}
5^x=1 <=> x=0
Система неравенств дает нам 5^x>=4 и 5^x<5
x>=log_5 {4} и x<1
Ответ: [log_5 {4}; 1) U {0}
Получаем, что методом интервалов решением будут t∈[4;5)U{1}
5^x=1 <=> x=0
Система неравенств дает нам 5^x>=4 и 5^x<5
x>=log_5 {4} и x<1
Ответ: [log_5 {4}; 1) U {0}
Похожие вопросы
Предмет: История,
автор: rilskijvasil77
Предмет: Геометрия,
автор: alinacamica
Предмет: Литература,
автор: alanibragimov
Предмет: Математика,
автор: azamatasdvip
Предмет: Алгебра,
автор: MAXIMUS12345