Предмет: Математика,
автор: mandarinka54
Здравствуйте, какой получается ответ в неравенстве?
Тест ЕГЭ по профильной математике, 15 задание
2^x- 6 - (9∙2^x-37 )/(4^x-7∙2^x+12)≤1/(2^x-4)
Приложения:
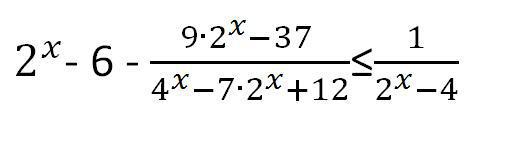
Ответы
Автор ответа:
0
Все, дошло.
В прошлый раз допустил ошибку, после замены и преобразований получаем:

Теперь числитель без проблем раскладывается на множители:

Решаем методом интервалов неравенство и получаем, что
t<=1; 3<t<4; 4<t<=8;
Тогда x<=0; log2(3)<x<2; 2<x<=3
В прошлый раз допустил ошибку, после замены и преобразований получаем:
Теперь числитель без проблем раскладывается на множители:
Решаем методом интервалов неравенство и получаем, что
t<=1; 3<t<4; 4<t<=8;
Тогда x<=0; log2(3)<x<2; 2<x<=3
Похожие вопросы