Предмет: Алгебра,
автор: Олька98
помогите с этой системой, бо'льшая проблема у меня с первым неравенством...
Приложения:
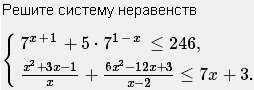
Ответы
Автор ответа:
0
Первое неравенство.
7*7^x - 35*7^(-x) - 246 <=0;
7^x = t;
7^(-x) = 1/t;
(7*t - 246/t + 35)/ t <=0; /*t>0;
7t^2 - 246 t + 35 <=0
D = 244^2;
t1 = 35;
t2= 1/7;
7(t-35)(t-1/7) <=0;
+ - +
____1/7____35_____t
1/7<= t<= 35;
7^(-1)<=7^x <=7^log7_35;
-1<= x <=log7_35;
Решением 1-го неравенства бeдет множество х [-1; 1+log7_5]
второе неравенство сначала упростим.
x^2/x + (3x-1)/x + 6x(x-2)/(x-2)) + 3/(x-2) <= 7x + 3;
x + (3x-1)/x + 6x + 3/(x-2) <= 7x + 3;
(3x -1)/x + 3/ (x-2) - 3 <=0;
3x^2 - 7x + 2 + 3x - 3x^2 + 6x / x(x-2) <=0;
2x+2/ x(x-2) <=0;
x+1/ x(x-2) <=0;
x= -1;
x=0;
x=2.
на коорд.прямой точки 0 и 2 выкалываем(из знаменателя), а точку х = -1 закрашиваем.
- + - +
_________[-1]______(0)______(2)______x
Решением 2-го неравенства будет множество х (- беск-сть; -1] U (0; 2)
Осталось пересечь решения 1 и 2 неравенств
________[-1]_____________[1+log7_5]______x
________[-1]______(0)________________(2)___x
Точка х = -1 есть в обоих решениях, Дополнительно интервал(0; 1+log7_5).
Ответ
{-1}; (0;1+log7_5)
7*7^x - 35*7^(-x) - 246 <=0;
7^x = t;
7^(-x) = 1/t;
(7*t - 246/t + 35)/ t <=0; /*t>0;
7t^2 - 246 t + 35 <=0
D = 244^2;
t1 = 35;
t2= 1/7;
7(t-35)(t-1/7) <=0;
+ - +
____1/7____35_____t
1/7<= t<= 35;
7^(-1)<=7^x <=7^log7_35;
-1<= x <=log7_35;
Решением 1-го неравенства бeдет множество х [-1; 1+log7_5]
второе неравенство сначала упростим.
x^2/x + (3x-1)/x + 6x(x-2)/(x-2)) + 3/(x-2) <= 7x + 3;
x + (3x-1)/x + 6x + 3/(x-2) <= 7x + 3;
(3x -1)/x + 3/ (x-2) - 3 <=0;
3x^2 - 7x + 2 + 3x - 3x^2 + 6x / x(x-2) <=0;
2x+2/ x(x-2) <=0;
x+1/ x(x-2) <=0;
x= -1;
x=0;
x=2.
на коорд.прямой точки 0 и 2 выкалываем(из знаменателя), а точку х = -1 закрашиваем.
- + - +
_________[-1]______(0)______(2)______x
Решением 2-го неравенства будет множество х (- беск-сть; -1] U (0; 2)
Осталось пересечь решения 1 и 2 неравенств
________[-1]_____________[1+log7_5]______x
________[-1]______(0)________________(2)___x
Точка х = -1 есть в обоих решениях, Дополнительно интервал(0; 1+log7_5).
Ответ
{-1}; (0;1+log7_5)
Автор ответа:
0
даа, у меня сошлось, спасибо :))
Похожие вопросы
Предмет: Английский язык,
автор: yegor151
Предмет: Русский язык,
автор: Аноним
Предмет: Обществознание,
автор: arinakrasnova705
Предмет: Математика,
автор: fedotov1979