Предмет: Алгебра,
автор: IR72016
Как решать??? 0_o Что делать???
Приложения:
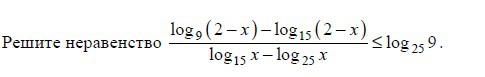
Ответы
Автор ответа:
0
ОДЗ:
х>0
2-x>0
Получаем 0<x<2
Перейти к другому основанию, например 10:


Справа

Неравенство примет вид

или

Так как

то


1) если х>1, а с учетом ОДЗ х∈(1;2)
логарифмическая функция возрастает и большему значению функции соответствует большее значение aргумента

2) если 0<x<1, то

х>0
2-x>0
Получаем 0<x<2
Перейти к другому основанию, например 10:
Справа
Неравенство примет вид
или
Так как
то
1) если х>1, а с учетом ОДЗ х∈(1;2)
логарифмическая функция возрастает и большему значению функции соответствует большее значение aргумента
2) если 0<x<1, то
Автор ответа:
0
Спасибо, а что дальше делать
Похожие вопросы
Предмет: Биология,
автор: SDAFFASFW
Предмет: Другие предметы,
автор: rafi44
Предмет: Математика,
автор: dfyziz18
Предмет: Литература,
автор: kopilovaarina
Предмет: Математика,
автор: psix4354