Предмет: Математика,
автор: reshetnikovz
Помогите решить задание. Ответ тоже прикреплён, но мне нужно решение, заранее спасибо
Приложения:
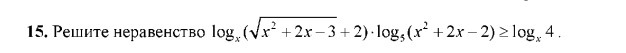

Ответы
Автор ответа:
0
1) Область определения логарифма
{ x > 0; x =/= 1
{ x^2 + 2x - 3 = (x + 3)(x - 1) > 0
Отсюда
{ x > 0; x =/= 1
{ x < -3 U x > 1
В итоге: x > 1
Это значит, что логарифм по основанию х - возрастающий.
Кроме того, если x^2 + 2x - 3 > 0. то x^2 + 2x - 2 тоже > 0
2) Теперь решаем само неравенство

По одному из свойств логарифмов

Причем новое основание с может быть каким угодно, например, 10.

Замена

Поскольку x > 1, то lg (x) > 0, поэтому при умножении на знаменатель знак неравенства не меняется.
lg(y + 2)*lg(y^2 + 1) >= lg(4)*lg(5)
Единственное решение уравнения: y = 2, тогда y + 2 = 4, y^2 + 1 = 5.
Решение неравенства: y >= 2
y = √(x^2 + 2x - 3) >= 2
x^2 + 2x - 3 >= 4
x^2 + 2x - 7 >= 0
D = 2^2 - 4(-7) = 4 + 28 = 32 = (4√2)^2
x1 = (-2 - 4√2)/2 = -1 - 2√2
x2 = (-2 + 4√2)/2 = -1 + 2√2
x ∈ (-oo; -1-2√2] U [-1+2√2; +oo)
Но по области определения x > 1
Ответ: x ∈ [2√2 - 1; +oo)
{ x > 0; x =/= 1
{ x^2 + 2x - 3 = (x + 3)(x - 1) > 0
Отсюда
{ x > 0; x =/= 1
{ x < -3 U x > 1
В итоге: x > 1
Это значит, что логарифм по основанию х - возрастающий.
Кроме того, если x^2 + 2x - 3 > 0. то x^2 + 2x - 2 тоже > 0
2) Теперь решаем само неравенство
По одному из свойств логарифмов
Причем новое основание с может быть каким угодно, например, 10.
Замена
Поскольку x > 1, то lg (x) > 0, поэтому при умножении на знаменатель знак неравенства не меняется.
lg(y + 2)*lg(y^2 + 1) >= lg(4)*lg(5)
Единственное решение уравнения: y = 2, тогда y + 2 = 4, y^2 + 1 = 5.
Решение неравенства: y >= 2
y = √(x^2 + 2x - 3) >= 2
x^2 + 2x - 3 >= 4
x^2 + 2x - 7 >= 0
D = 2^2 - 4(-7) = 4 + 28 = 32 = (4√2)^2
x1 = (-2 - 4√2)/2 = -1 - 2√2
x2 = (-2 + 4√2)/2 = -1 + 2√2
x ∈ (-oo; -1-2√2] U [-1+2√2; +oo)
Но по области определения x > 1
Ответ: x ∈ [2√2 - 1; +oo)
Похожие вопросы
Предмет: Математика,
автор: kuznecovakarolina265
Предмет: Физика,
автор: Demonster228
Предмет: Химия,
автор: masha804112
Предмет: Математика,
автор: annagromova02
Предмет: Физика,
автор: ma1999ma