Question

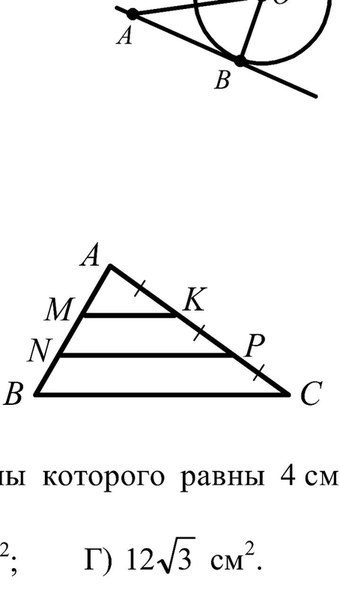
Прямые MK и NP, пересекающие стороны
треугольника ABC, изображенного на рисунке,
параллельны, AK = KP = PC, MK = 6 см. Чему равна длина стороны BC треугольникаА) 8 см; Б) 18 см; В) 16 см; Г) 24 см

Answer 1

1) MK II BC, т.к. они отсекают равные отрезки на прямой AC (теорема Фалеса)
2) ΔAMK ~ ΔABC, т.к ∠A общий, ∠AMK = ∠ABC (соответственные при MK II BC и секущей AB), ∠AKM = ∠ACB (аналогично при секущей АС).
3) Т.к ΔAMK ~ ΔABC, то  MK/BC = AK/AC = 1/3. BC = 3MR = 18 см.

Ответ: Б) 18 см.