Предмет: Алгебра,
автор: Таня1888
помогите пожалуйста!!Найти радиус и интервал сходимости степенного ряда
Приложения:
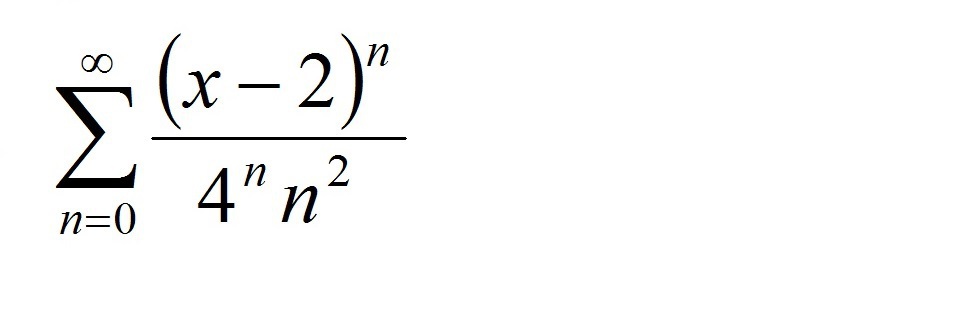
Ответы
Автор ответа:
0
Решение в приложении.
Приложения:

Автор ответа:
0
Радиус сходимости найдём по формуле Коши(рис 1):
![R=lim_{ntoinfty}sqrt[n]{frac{1}{4^n*n^2}}=frac{1}{4}\r=frac{1}{R}=4 R=lim_{ntoinfty}sqrt[n]{frac{1}{4^n*n^2}}=frac{1}{4}\r=frac{1}{R}=4](https://tex.z-dn.net/?f=R%3Dlim_%7Bntoinfty%7Dsqrt%5Bn%5D%7Bfrac%7B1%7D%7B4%5En%2An%5E2%7D%7D%3Dfrac%7B1%7D%7B4%7D%5Cr%3Dfrac%7B1%7D%7BR%7D%3D4)
Интервал сходимости:
|x-2|<4
x-2<4 ; x-2>-4
x<6 ; x>-2
x∈(-2;6)
Но мы не знаем сходиться ли ряд на концах отрезка.
Остаётся это проверить.

Используем признак Лейбница для знакочередующих рядов(рис 3).
Функция монотонна и:
монотонна и:

Следовательно ряд сходится.

Это обобщённый гармонический ряд(рис 2). α>1 - ряд сходиться.
Интервал сходимости степенного ряда :
:
![xin [-2;6] xin [-2;6]](https://tex.z-dn.net/?f=xin+%5B-2%3B6%5D)
Интервал сходимости:
|x-2|<4
x-2<4 ; x-2>-4
x<6 ; x>-2
x∈(-2;6)
Но мы не знаем сходиться ли ряд на концах отрезка.
Остаётся это проверить.
Используем признак Лейбница для знакочередующих рядов(рис 3).
Функция
Следовательно ряд сходится.
Это обобщённый гармонический ряд(рис 2). α>1 - ряд сходиться.
Интервал сходимости степенного ряда
Приложения:



Похожие вопросы
Предмет: Математика,
автор: 0tyryrtfuhtyryrjruty
Предмет: Геометрия,
автор: natali280606
Предмет: Русский язык,
автор: neznaushly
Предмет: Обществознание,
автор: 010503030501
Предмет: Математика,
автор: sergeysmotrov03