Предмет: Алгебра,
автор: shakha2017
решайте тригонометрическую уравнению 2sin2x+cos2x=1
Ответы
Автор ответа:
0
решение в скане.......
Приложения:
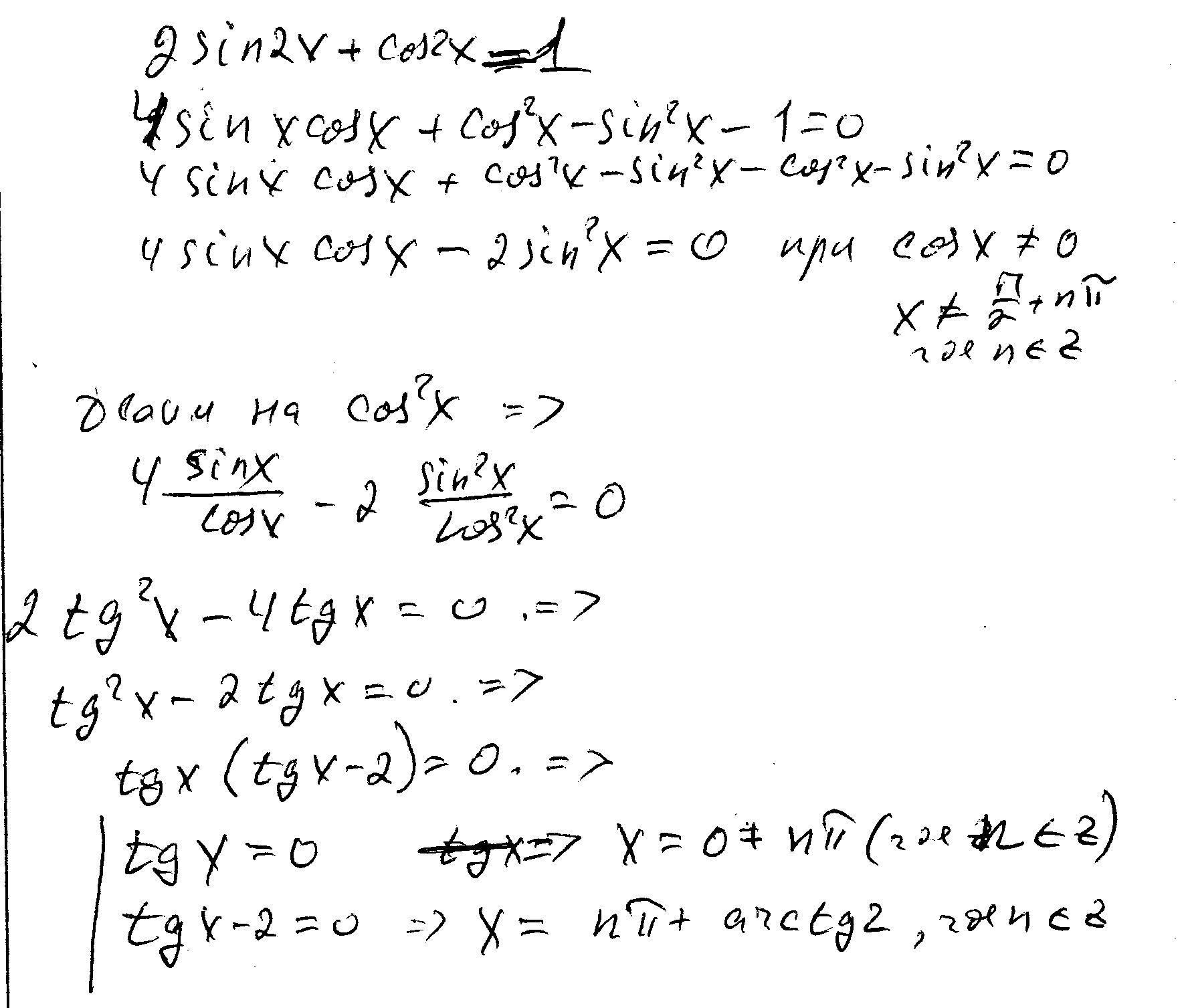
Автор ответа:
0
4sinx cosx + cos^2 x-sin^2 x = cos^2 x+sin^2 x
4 sinx cosx +cos^2 x-sin^2 x-cos^2 x-sin^2x = 0
4sinxcosx-2sin^2 x=0
2sinx(2cosx-sinx)=0
sinx =0 или 2cosx-sinx=0
x=пn 2ctgx-1=0 (разделили всё на sinx)
ctgx=1/2
x=arcctg1/2 +пn
Ответ: пn; arcctg1/2+пn
Приложения:
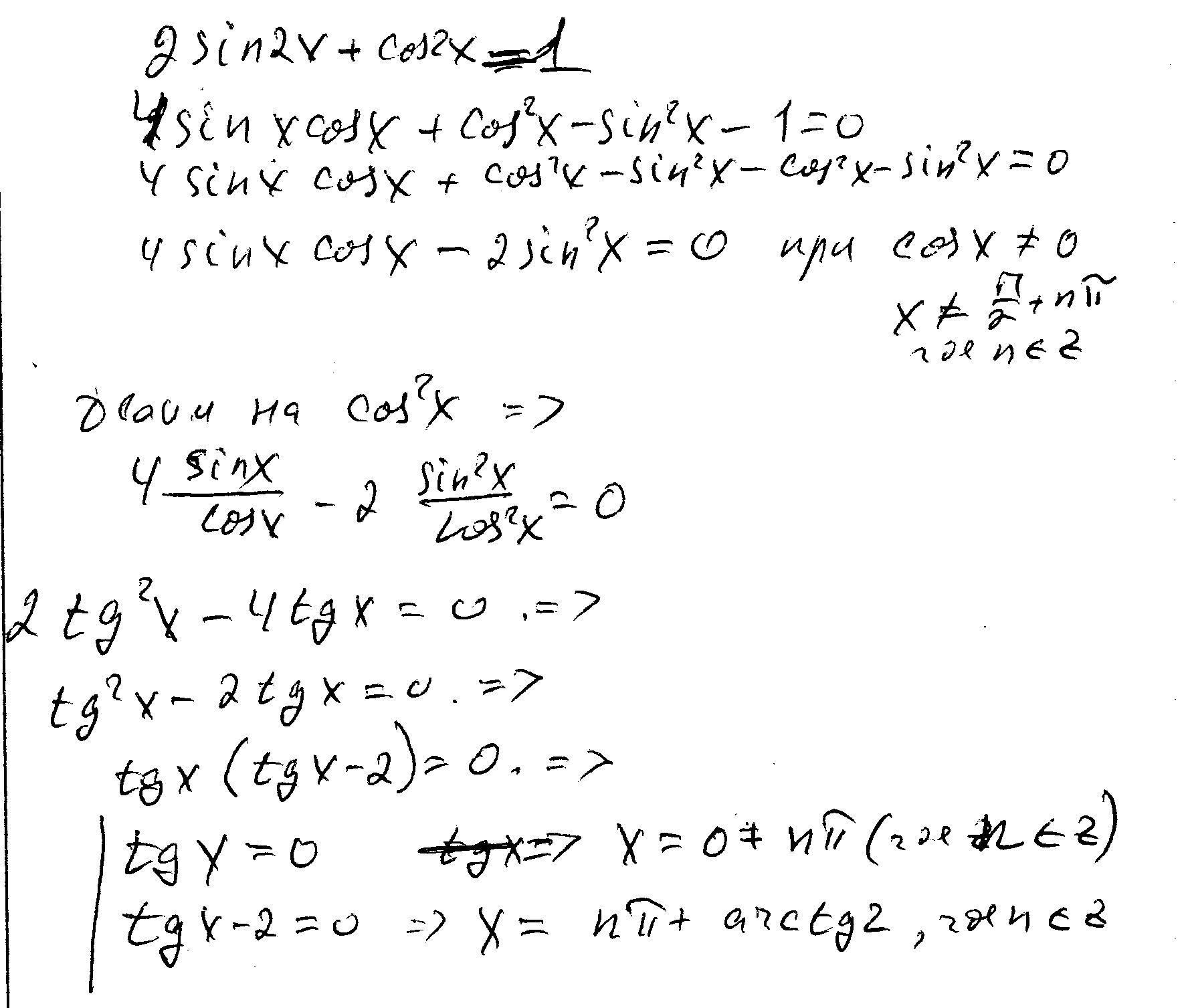
Похожие вопросы
Предмет: Математика,
автор: PinkCoffee
Предмет: Алгебра,
автор: prostomatv
Предмет: Математика,
автор: Illia12334
Предмет: Биология,
автор: 1shad11
Предмет: Алгебра,
автор: Nikishon