Предмет: Алгебра,
автор: StyKO
Дифференциальное уравнение
Приложения:
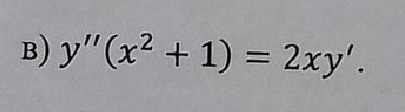
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: 25kozachok25
Предмет: Биология,
автор: lublus2
Предмет: История,
автор: dimaop03
Предмет: Математика,
автор: vitalik303
Предмет: Химия,
автор: ynasha87