Предмет: Геометрия,
автор: maidose
СРОЧНО ПОМОГИТЕ !!!! ДАЮ 25 БАЛЛОВ !Основание равнобедренного треугольника равно 4 см а боковые стороны по 10 см . В треугольнике вписана окружность , а к этой окружности проведена касательная , которая пересекает боковые стороны . Найдите периметр треугольника , который отсекает касательная.
Ответы
Автор ответа:
0
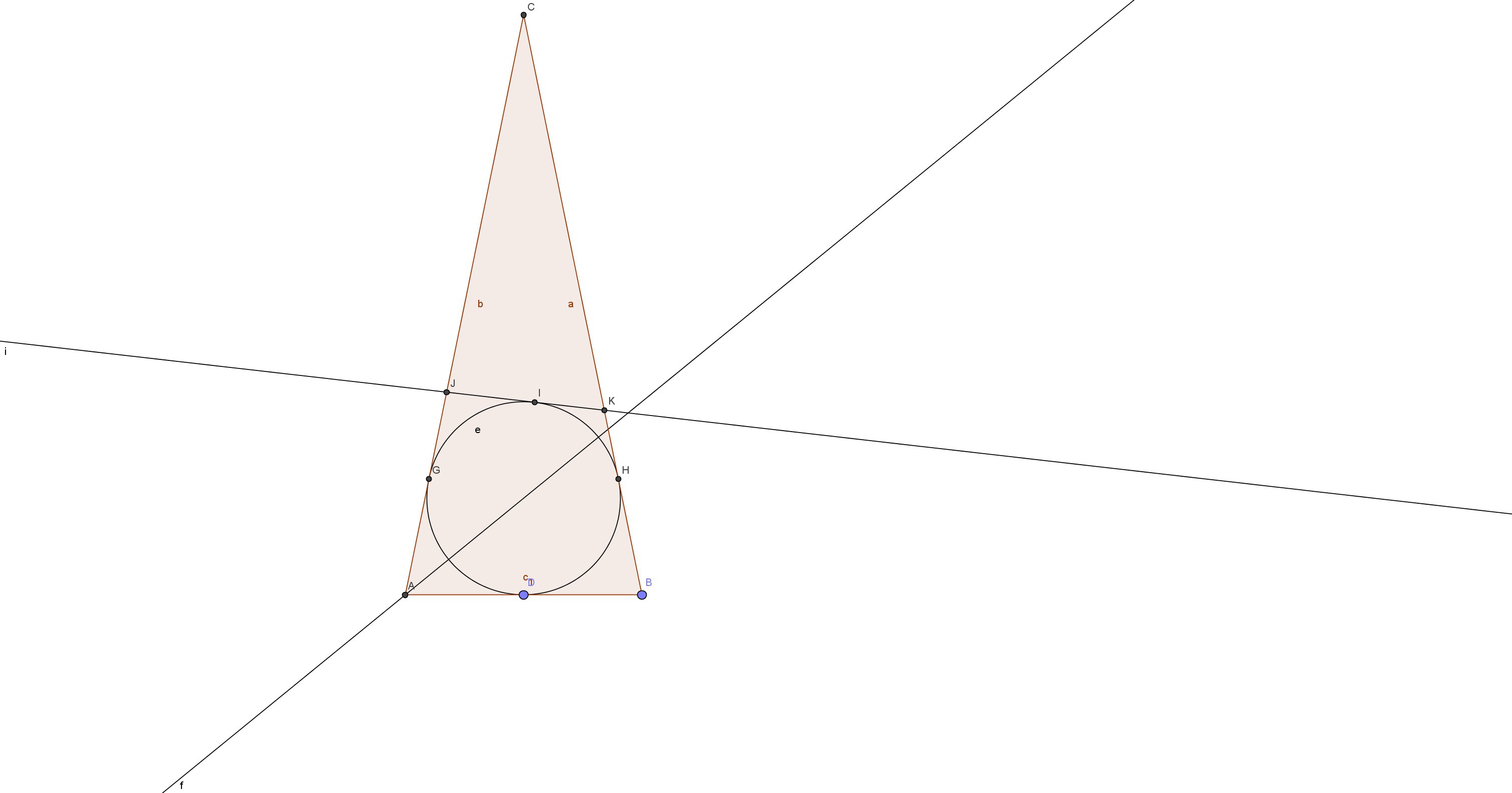
Найти периметр треугольника CJK
Т.к. отрезки касательных проведенные из одной точки равны, то JG=JI и IK = IH => периметр СJK = CG + CH, CG = CH и AG=AD и DB=BH => периметр CJK = 2 * CG, ABC - равнобедренный => AD=DB=2, AC = 10 = AG + GC => GC = 8 => периметр = 16
Т.к. отрезки касательных проведенные из одной точки равны, то JG=JI и IK = IH => периметр СJK = CG + CH, CG = CH и AG=AD и DB=BH => периметр CJK = 2 * CG, ABC - равнобедренный => AD=DB=2, AC = 10 = AG + GC => GC = 8 => периметр = 16
Приложения:
Автор ответа:
0
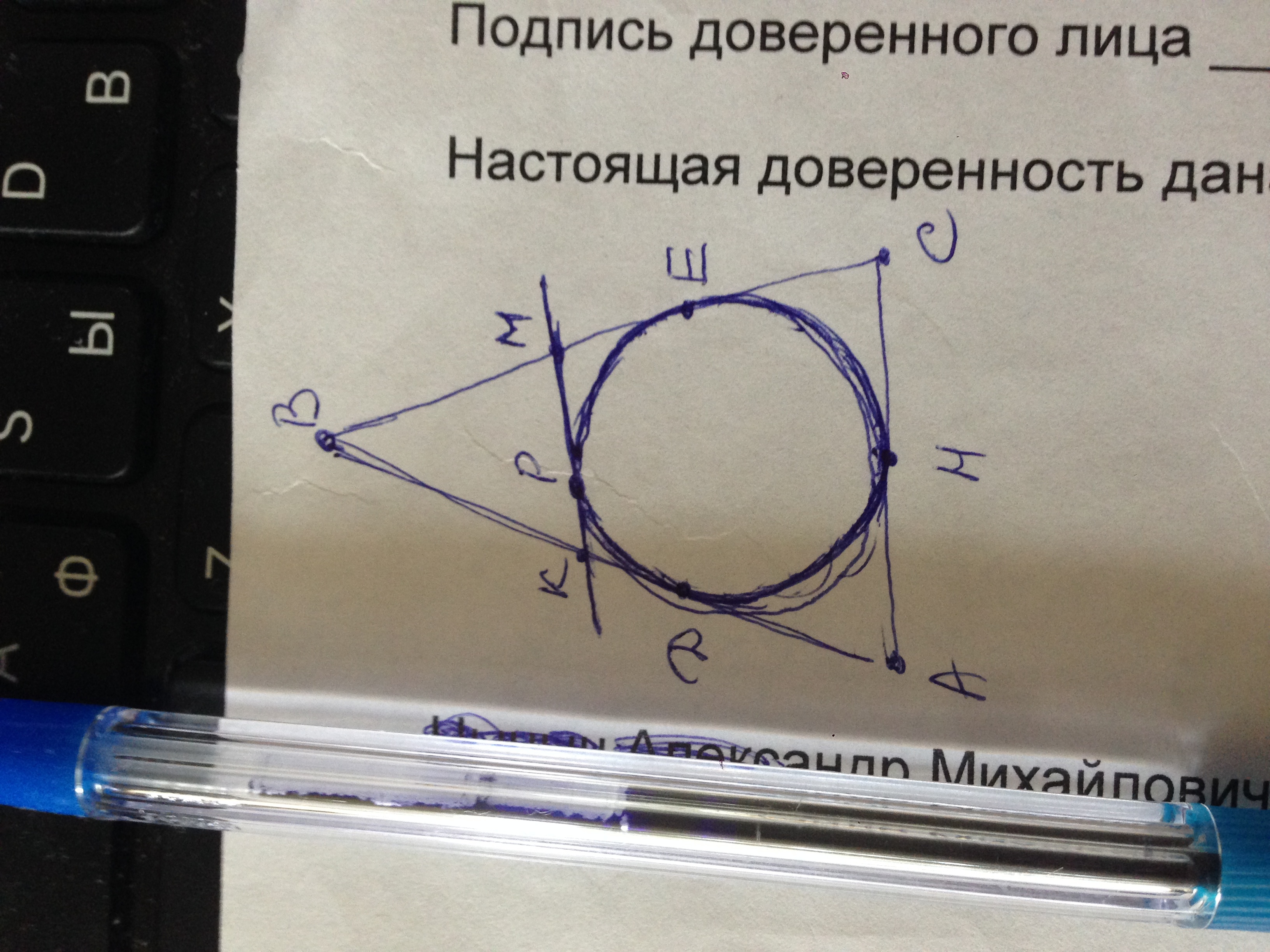
В тр-ке АВС АВ=ВС=10 см, АС=4 см, Касательная пересекает стороны АВ и ВС в точках К и М, касаясь окружности в точке Р.
В треугольнике АВС Вписанная окружность касается сторон АВ ВС и АС в точкахД, Е и Н соответственно.
АД=АН, ВД=ВЕ, СЕ=СН так как они касательные к окружности из одной точки попарно.
АН=АС/2=4/2=2 см
ВД=АВ-АН=10-2=8 см. ВД=ВЕ.
В треугольнике ВКМ ВК+КР=ВК+КД=ВД (КД=КР как касательные), ВМ+РМ=ВМ+МЕ=ВЕ (РМ=МЕ как касательные), значит периметр тр-ка
ВКМ=ВД+ВЕ=8+8=16 см
В треугольнике АВС Вписанная окружность касается сторон АВ ВС и АС в точкахД, Е и Н соответственно.
АД=АН, ВД=ВЕ, СЕ=СН так как они касательные к окружности из одной точки попарно.
АН=АС/2=4/2=2 см
ВД=АВ-АН=10-2=8 см. ВД=ВЕ.
В треугольнике ВКМ ВК+КР=ВК+КД=ВД (КД=КР как касательные), ВМ+РМ=ВМ+МЕ=ВЕ (РМ=МЕ как касательные), значит периметр тр-ка
ВКМ=ВД+ВЕ=8+8=16 см
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: baevaanna084
Предмет: Математика,
автор: ustinovbogdan62
Предмет: Математика,
автор: misheelterkh
Предмет: Математика,
автор: sachaparh