Предмет: Геометрия,
автор: ch1ckenn
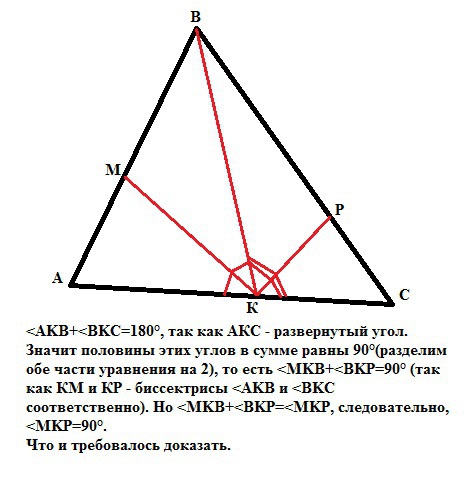
На сторонах AB, BC, AC треугольника ABC взяты точки M, P , K соответственно, так что лучи KM и KP являются биссектрисами углов AKB и BKC. Докажите, что угол MKP=90 (+ рисунок/картинка)
Ответы
Автор ответа:
0
<AKB+<BKC=180°, так как АКС - развернутый угол.
Значит половины этих углов в сумме равны 90°(разделим обе части уравнения на 2), то есть <MKB+<BKP=90° (так как КМ и КР - биссектрисы <AKB и <BKC соответственно). Но <MKB+<BKP=<MKP, следовательно, <MKP=90°.
Что и требовалось доказать.
Значит половины этих углов в сумме равны 90°(разделим обе части уравнения на 2), то есть <MKB+<BKP=90° (так как КМ и КР - биссектрисы <AKB и <BKC соответственно). Но <MKB+<BKP=<MKP, следовательно, <MKP=90°.
Что и требовалось доказать.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: vladusbro670
Предмет: Русский язык,
автор: ivan49311209
Предмет: Математика,
автор: hahshdhdhd
Предмет: Литература,
автор: Ксения2001010
Предмет: Математика,
автор: Аноним