Question

В сосуде, имеющий форму конуса, уровень жидкости достигает 6/7 высоты. Объем сосуда 3430 мл. Чему равен объём налитой жидкости? Ответ дайте в миллиметрах.

Answer 1

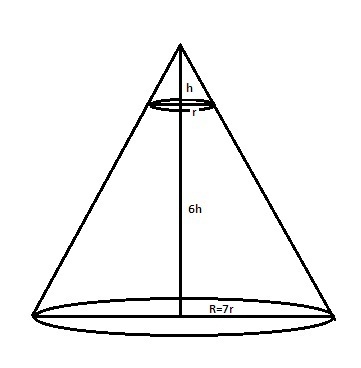
Вот на рисунке этот конус, заполненный на 6/7 высоты.
Треугольники из радиуса, высоты и образующей подобны друг другу, поэтому:
1) Высота над уровнем жидкости равна h, а высота жидкости 6h.
То есть высота всего сосуда равна H = 7h.
2) Радиус поверхности жидкости равен r, а радиус основания R = 7r.
3) Объем части над поверхностью
v = 1/3*pi*r^2*h
Объем всего сосуда
V = 1/3*pi*R^2*H = 1/3*pi*(7r)^2*7h = 7^3*v = 343*v = 3430
Объем части сосуда над поверхностью
v = 10 мл.
Объем жидкости
V - v = 3430 - 10 = 3420 мл.