Question

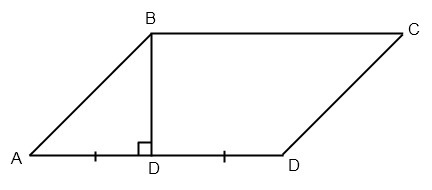
найдите площадь параллелограмма ABCD у которого один из углов равен 45 , высота BE проведенная из вершины тупого угла равна 3.2 см и делит сторону AD на две равные части

Answer 1

1) в треугольнике АВЕ угол А равне 45°, угол Е- прямой, следовательно угол АВЕ равен углу А = 45. По признаку равнобедренного треугольника этот треугольник равнобедренный с основанием АВ. 2) По определению равноб. треугольника АЕ равно ВЕ равно 3,2. 3) АD = 2АЕ = 2 × 3,2 = 6,4см. 4) площадь параллелограмма равна произведению высоты и основания, к которому эта высота проведена. Площадь АВСD = 3.2 × 6,4 = 20,48 см²

Answer 2

∠ABD = 90° - ∠BAD = 45°
∠ABD = ∠BAD ⇒ ΔABD - равнобедренный (по свойству) ⇒
AD = BD = 3,2 см
AD = 2AD = 6,4 см
S = AD · BD = 6,4 см · 3,2 см = 20,48 см²
Ответ: 20,48 см²