Предмет: Математика,
автор: 07Кузя35
Диагональ боковой развёртки цилиндра равна 24 см , угол, между диагоналями обращенные основанию 150градусов. Найдите объем цилиндра
Ответы
Автор ответа:
0
Приложения:
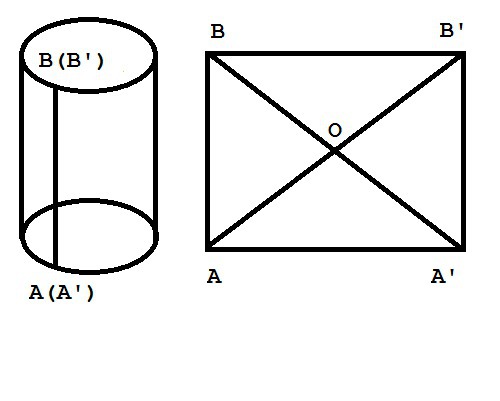
Похожие вопросы
Предмет: Математика,
автор: dimamangiir
Предмет: Українська мова,
автор: lysia192
Предмет: Химия,
автор: aacenko65
Предмет: Литература,
автор: marina1114
Предмет: Алгебра,
автор: mscannonball