Предмет: Алгебра,
автор: yaltis
Построите график функции y=  и определите, при каких значениях m прямая y=m не имеет с графиком общих точек. Решите, пожалуйста, подробно, с пошаговым объяснением.
и определите, при каких значениях m прямая y=m не имеет с графиком общих точек. Решите, пожалуйста, подробно, с пошаговым объяснением.
Ответы
Автор ответа:
0
Находим область определения функции:
Теперь можно выполнить упрощение:
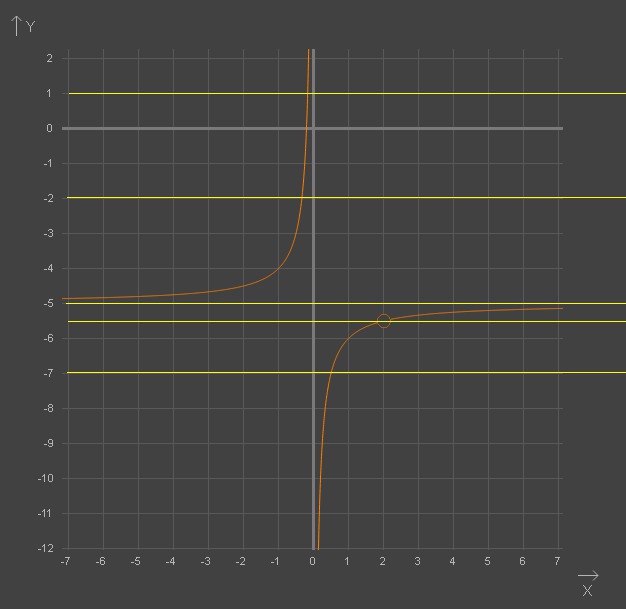
Данный график представляет собой гиперболу
Прямая
Прямая
Ответ: -5 и -5,5
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: Dilyara567
Предмет: Математика,
автор: vekatte
Предмет: Алгебра,
автор: mrdamixyt8250
Предмет: Математика,
автор: milshka
Предмет: История,
автор: mamashka1111