Question

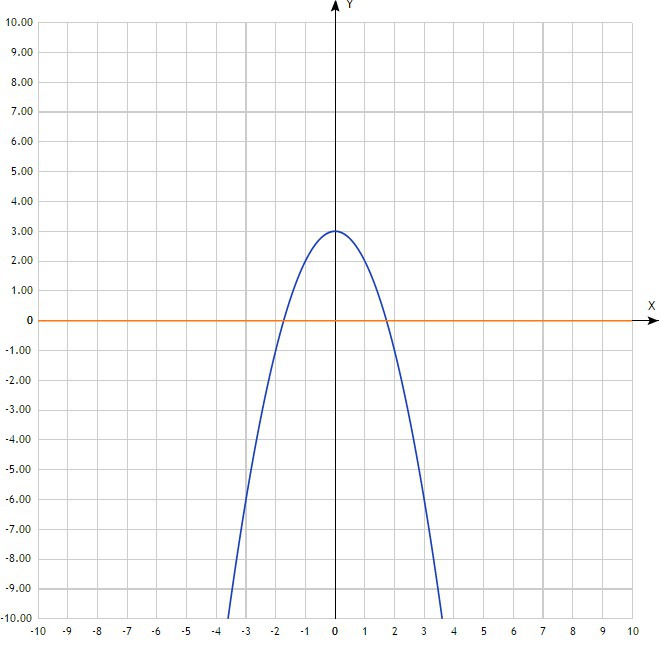
Вычислить площадь фигуры, ограниченной линиями: у=-х²+3, у=0

Answer 1

С точки зрения геометрии площадь фигуры это определённый интеграл. Необходимо построить чертёж для зрительного восприятия. у=0 это ось ОХ. Нас интересует фигура над осью ОХ (см. чертёж во вложении), чтобы найти её площадь надо найти точки пересечения с осью ОХ, то есть
-x²+3=0
-x²=-3
x²=3
x=√3     x=-√3
Теперь можем найти площадь
$S= intlimits^{ sqrt{3}} _ {-sqrt{3}} {(-x^2+3)} , dx = - frac{x^3}{3} +3x| _{ -sqrt{3} }^{ sqrt{3} }=- frac{3sqrt{3} }{3}+3 sqrt{3} - frac{3sqrt{3} }{3}+3 sqrt{3}=$$- sqrt{3}+3 sqrt{3}- sqrt{3}+3 sqrt{3}=4 sqrt{3}$≈6,93 ед²