Предмет: Геометрия,
автор: AnekdotArina
Помогите, очень надо!
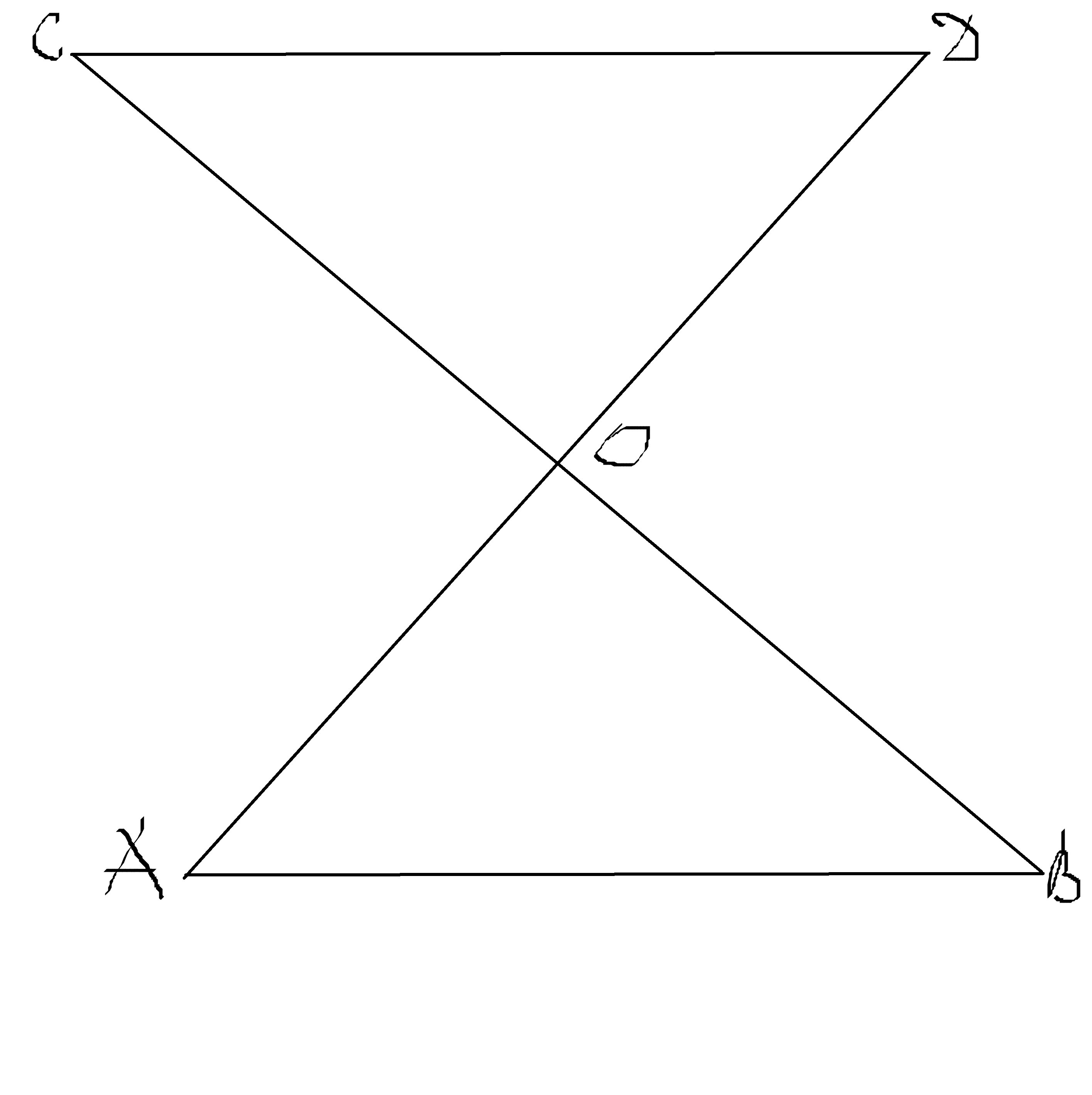
Докажите равенство отрезков AO и OD, изображенных на рисунке, если AB параллельно CD и BO=CO.
Приложения:
Ответы
Автор ответа:
0
1. CO=OB;
∠AOB=∠COD, т. к. вертикальные;
∠OCD=∠OBA, т. к. накрест лежащие углы, при пересечении двух параллельных прямых секущей, равны.⇒ ΔCOD=ΔBOA (по стороне и прилежащим к ней углам).
2. В равных треугольниках равные элементы равны, следовательно AO=OD.
∠AOB=∠COD, т. к. вертикальные;
∠OCD=∠OBA, т. к. накрест лежащие углы, при пересечении двух параллельных прямых секущей, равны.⇒ ΔCOD=ΔBOA (по стороне и прилежащим к ней углам).
2. В равных треугольниках равные элементы равны, следовательно AO=OD.
Автор ответа:
0
Спасибо вам!
Автор ответа:
0
Пожалуйста)
Похожие вопросы
Предмет: Математика,
автор: pupsik119
Предмет: Алгебра,
автор: djhdbdb
Предмет: Українська мова,
автор: babiynasta
Предмет: Биология,
автор: svetakuz1