Предмет: Математика,
автор: Alexiay
Методом математической индукции по n ∈ N доказать
Приложения:
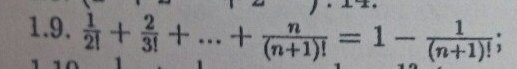
Ответы
Автор ответа:
0
Докажем равенство методом математической индукции:
1) Проверим справедливость равенства для n=1
Равентство справедливо
2) Предположим что равенство справедливо для n=k
докажем справедливость равенства для n=k+1
т.к. равенство справедливо для n=k+1
Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального n.
Похожие вопросы
Предмет: Геометрия,
автор: f7g7f7fufo
Предмет: Українська література,
автор: nastja14032009
Предмет: Математика,
автор: ozhnyu
Предмет: Алгебра,
автор: andytazin
Предмет: География,
автор: Красотка124841612