Question

. Площадь прямоугольного треугольника равна
(50* корень из 3)/3. Один из острых углов равен 60.
Найдите длину катета, лежащего напротив этого угла. Решить надо не через тангенс, помогите пожалуйста, и опишите решение

Answer 1

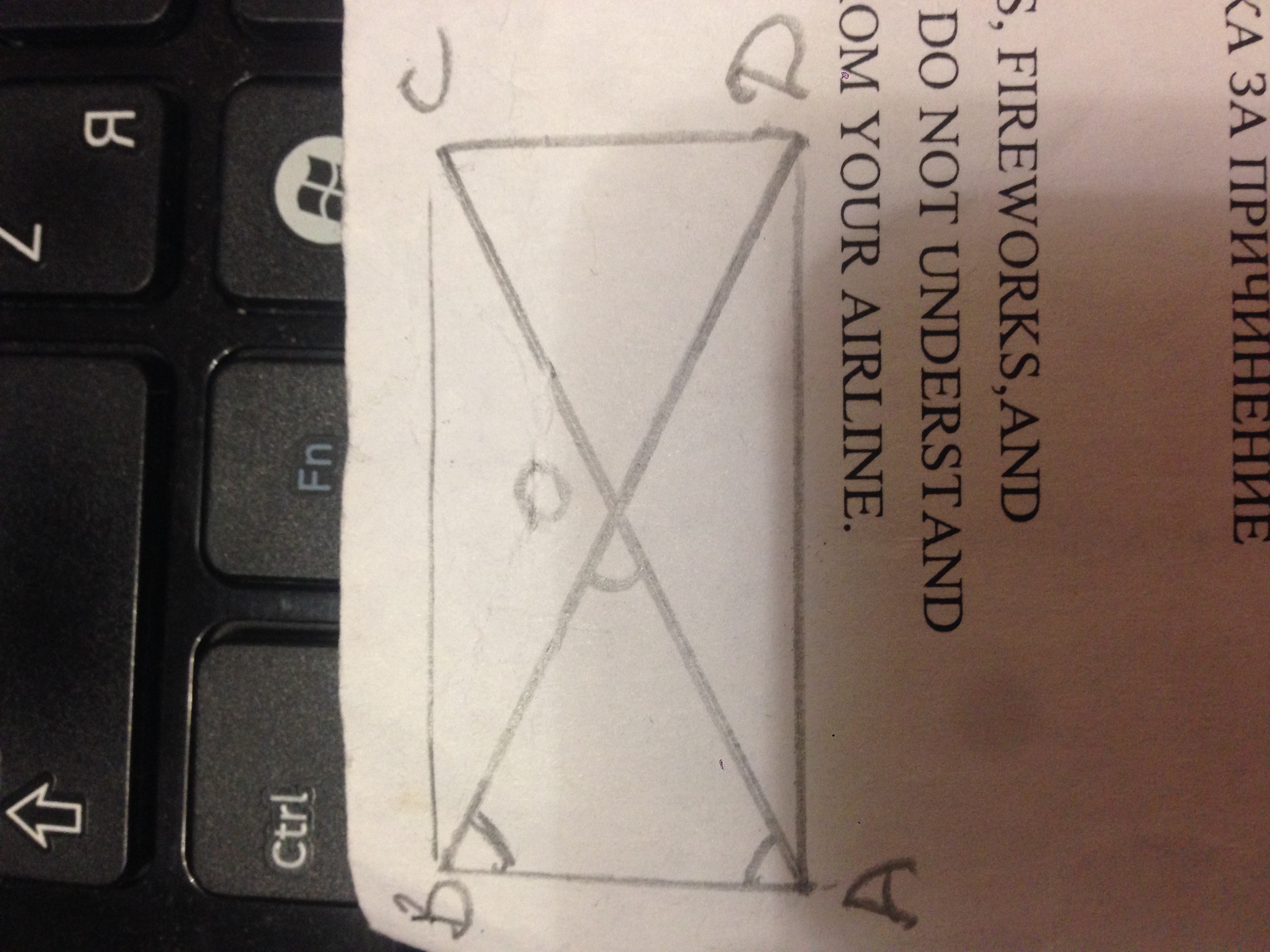
В тр-ке АВД ∠А=90°, ∠В=60°.
Достроим треугольник до прямоугольника АВСД, в котором ВД  и АС - диагонали.
ΔАВД=ΔВСД .
Площадь прямоугольника равна: Sпр=2S(АВД)=100√3/3.
В тр-ке АВО ∠АВО=∠ВАО=∠АОВ=60°.
Площадь прямоугольника через диагонали равна: 
Sпр=(d²·sin60)/2=(AC²·sin60)/2, ⇒ АС²=2S/sin60=2·2·100√3/3√3=400/3.
АС=√(400/3)=20√3/3.
В тр-ке АВС катет АВ лежит напротив угла в 30°, значит он вдвое короче гипотенузы.
АВ=АС/2=10√3/3.
По т. Пифагора ВС²=АС²-АВ²=(1200-300)/9=100.
ВС=АД=10 - это ответ.