Предмет: Математика,
автор: Lalala3510
СРОЧНО НУЖНО, ПРОТОТИП ЗАДАНИЯ 23 ИЗ ОГЭ . ТОМУ КТО РЕШИТ ЗАРАНЕЕ СПАСИБО)
постройте график функции -2х+4|х|-х^2
и определите, при каких
значениях с прямая
у =c
имеет с графиком ровно три общие точки.
Ответы
Автор ответа:
0
В функции у = -2х+4|х|-х^2 раскроем модуль:
у = -2х+4х-х^2 = -х² + 2х = -х(х - 2), х ≥ 0.
у = -2х - 4х -х² = -х² - 6х = -х(х + 6), х ≤ 0.
Графики этих функций - параболы ветвями вниз (коэффициенты при х² отрицательны).
Найдём их вершины по формуле хо = -в/2а:
хо1 = -2/2*(-1) = 1, уо1 = -1+2*1 = 1,
хо2 = 6/2*(-1) = -3. уо2 = -9+6*3 = 9.
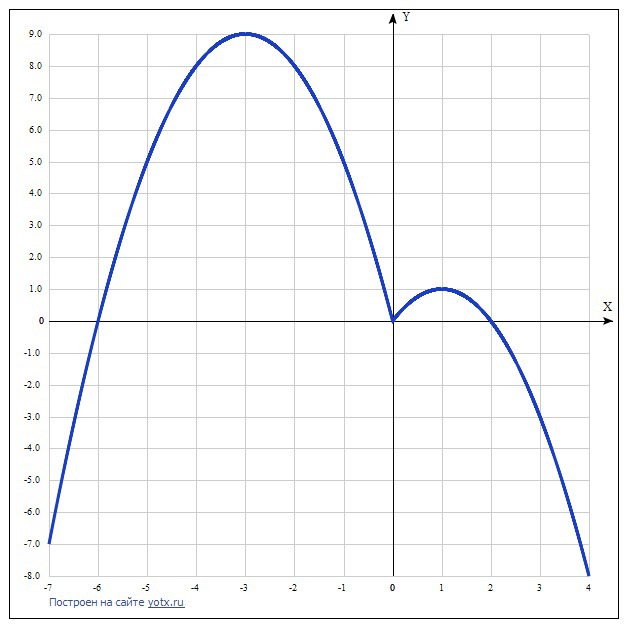
По графику видно, что три общие точки будут при c = 0 и при c = 1.
у = -2х+4х-х^2 = -х² + 2х = -х(х - 2), х ≥ 0.
у = -2х - 4х -х² = -х² - 6х = -х(х + 6), х ≤ 0.
Графики этих функций - параболы ветвями вниз (коэффициенты при х² отрицательны).
Найдём их вершины по формуле хо = -в/2а:
хо1 = -2/2*(-1) = 1, уо1 = -1+2*1 = 1,
хо2 = 6/2*(-1) = -3. уо2 = -9+6*3 = 9.
По графику видно, что три общие точки будут при c = 0 и при c = 1.
Приложения:
Похожие вопросы
Предмет: Литература,
автор: Vsevolod0903
Предмет: История,
автор: ssarkic12
Предмет: Математика,
автор: komeristayaolga2008
Предмет: Математика,
автор: konstantinzenk