Question

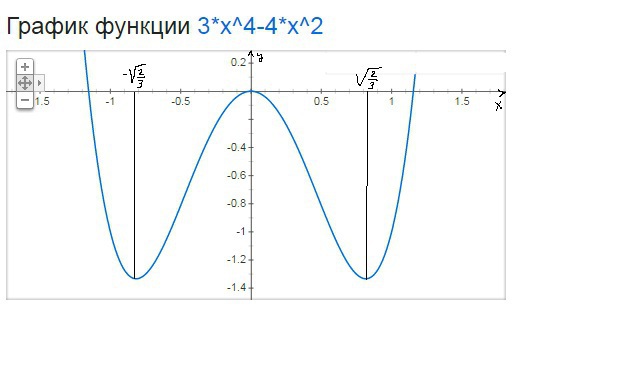
Исследовать на максимум и минимум y=3x^4-4x^2

Answer 1

y'=12x³-8x
y'=0
4x(3x²-2)=0
x=0, x=+-√(2/3)
√2/3≈0,8
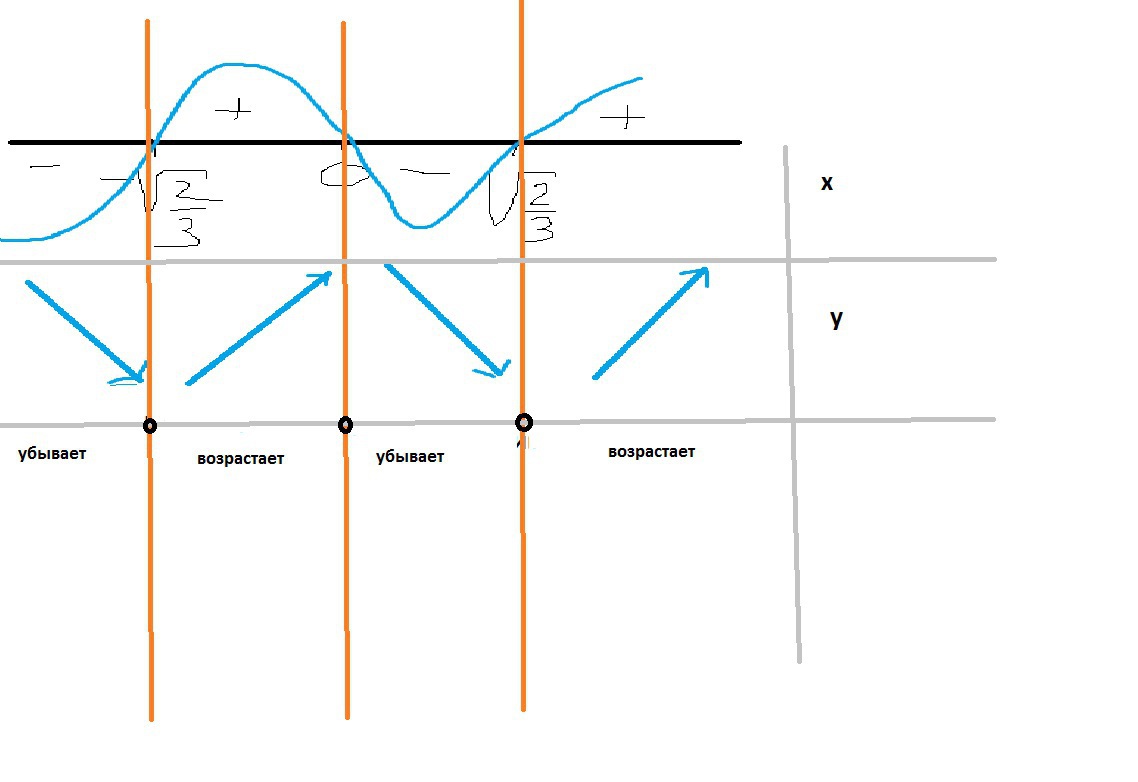
исследуем методом интервалов
нанесем значения в которых производная =0 на числовую ось и
рассмотрим знаки производной в интервалах 
при x>√2/3 например x=1 y'=12-8=4>0
при 0<х<√2/3  например х=0,5  y'=12*0.125-8*0,5=1,5-4=-2,5 <0
при -√2/3<x<0 например х=-0,5 y'=-1,5+4=2.5>0
при х<√2/3 например х=-1 y'=-12+8=-4<0 
1) в точках где производная меняет знак с - на + минимум это точки
х=-√(2/3)   и х=√(2/3) 
2) в точке где производная меняет знак с - на + максимум это точка х=0