Предмет: Алгебра,
автор: RollingStone
Решить уравнение (см. вложение) и найти все его корни, принадлежащие определенному отрезку, 10 класс.
Приложения:
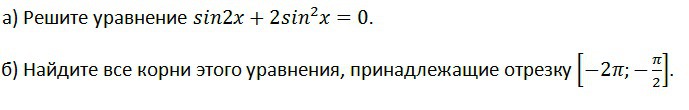
Ответы
Автор ответа:
0
sin2x+2sin²x=0
2sinxcosx+2sin²x=0
2sinx(cosx+sinx)=0
sinx=0⇒x=πn,n∈z
-2π≤πn≤-π/2
-4≤2n≤-1
-2≤n≤-1/2
n=-2⇒x=-2π
n=-1⇒x=-π
sinx+cosx=0/cosx
tgx+1=0⇒tgx=-1⇒x=-π/2+πk,k∈z
-2π≤-π/2+πk≤-π/2
-4≤-1+2k≤-1
-3≤2k≤0
-3/2≤k≤0
k=-1⇒x=-π/2-π=-3π/2
k=0⇒x=-π/2
2sinxcosx+2sin²x=0
2sinx(cosx+sinx)=0
sinx=0⇒x=πn,n∈z
-2π≤πn≤-π/2
-4≤2n≤-1
-2≤n≤-1/2
n=-2⇒x=-2π
n=-1⇒x=-π
sinx+cosx=0/cosx
tgx+1=0⇒tgx=-1⇒x=-π/2+πk,k∈z
-2π≤-π/2+πk≤-π/2
-4≤-1+2k≤-1
-3≤2k≤0
-3/2≤k≤0
k=-1⇒x=-π/2-π=-3π/2
k=0⇒x=-π/2
Автор ответа:
0
Огромное спасибо!!
Похожие вопросы
Предмет: Биология,
автор: Tijcfujv
Предмет: Физика,
автор: larisaholikulova
Предмет: Английский язык,
автор: sykochevaolga78
Предмет: Математика,
автор: alina07111
Предмет: Химия,
автор: grigoryanlilik