Предмет: Геометрия,
автор: 098Tin
Найдите длину окружности, описанной около прямоугольника, меньшая сторона которого равна 8 см, а угол между диагоналями равен a
Ответы
Автор ответа:
0
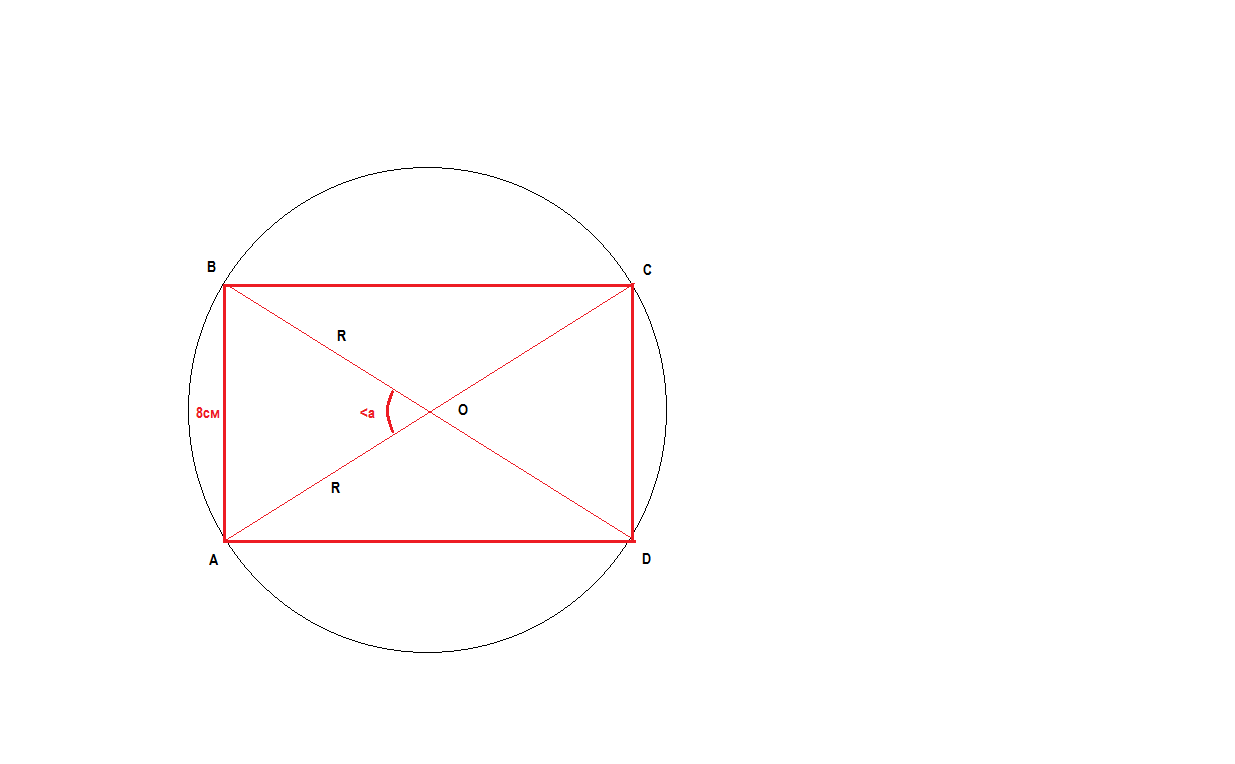
сделаем построение по условию
треугольник АОВ -равнобедренный
по теореме косинусов
AB^2 = R^2+R^2 - 2R^2*cos<a
АВ= 8 см
8^2 = 2R^2(1 -cos<a)
R^2 =8^2 /(2(1 -cos<a))
R =8 / √(2(1 -cos<a)) - радиус окружности
длина окружности C =2п*R = 2п*8 / √(2(1 -cos<a)) =16п / √(2(1 -cos<a))
ответ 16п / √(2(1 -cos<a))
** возможна запись другой формулой
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Nikola007007
Предмет: История,
автор: nurjanatjanarb92
Предмет: Математика,
автор: tokpaew31
Предмет: Математика,
автор: Аноним