Предмет: Математика,
автор: 20artem01
1) Найдите радиус окружности, вписанной в равносторонний треугольник со стороной 12 см
2) в четырехугольнике ABCD, описанном около около окружности, АВ=8 см, CD= 13 DA=16 см. Найдите см, сторону ВС
Ответы
Автор ответа:
0
т.к. треуг. АВС равносторонний, то СМ и АК являются одновременно биссектрисой, медианой и высотой.
Следовательно.
1)АМ=МВ=1/2*АВ=1/2*12=6см.
2) угол АМО=угол АМС=90 градусов.
3) угол АМК=КАС=60/2=30 градусам.
Рассмотрим треугольник АМО. Он прямоугольный. АМ=6, угол МАО=30град.
ОМ=АМ*tg30°=6*√3/3=2√3
ОМ это радиус вписанной окружности
2)В описанном выпуклом четырехугольнике суммы противоположных сторон равны.
ВС+АД=АВ+СД
ВС=АВ+СД-АД
ВС=8+16-13=11см
Следовательно.
1)АМ=МВ=1/2*АВ=1/2*12=6см.
2) угол АМО=угол АМС=90 градусов.
3) угол АМК=КАС=60/2=30 градусам.
Рассмотрим треугольник АМО. Он прямоугольный. АМ=6, угол МАО=30град.
ОМ=АМ*tg30°=6*√3/3=2√3
ОМ это радиус вписанной окружности
2)В описанном выпуклом четырехугольнике суммы противоположных сторон равны.
ВС+АД=АВ+СД
ВС=АВ+СД-АД
ВС=8+16-13=11см
Приложения:
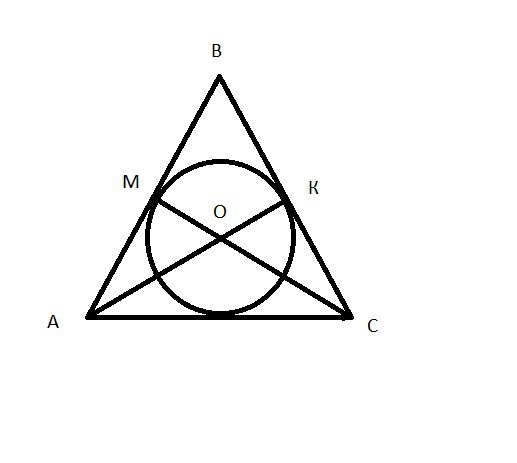
Похожие вопросы
Предмет: Физика,
автор: amir05d
Предмет: Физика,
автор: dzre
Предмет: Математика,
автор: ggawp2561
Предмет: Физика,
автор: kuznecovaa69
Предмет: Математика,
автор: paulina2