Предмет: Геометрия,
автор: Hodykin
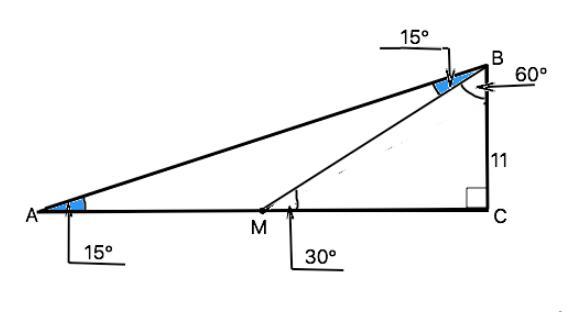
В треугольнике ABC известно, что угол C=90°, угол A=15°, BC=11 см. На катете AC отметили точку M так, что угол BMC=30°. Найдите отрезок AM.
Помогайте )
Ответы
Автор ответа:
0
Ответ: 22 см
Объяснение (подробно):
Сумма острых углов прямоугольного треугольника равна 90° ( т.е. без прямого угла) .
Острый угол А=15°, ⇒ острый угол В=90°-15°=75°. По условию в прямоугольном ∆ ВМС угол ВМС=30° ⇒ ∠МВС=60°. В ∆ МВС катет ВС противолежит углу 30°, ⇒ гипотенуза МВ=2•ВС=22 см (свойство)
∠АВМ=∠АВС -∠МВС=75°-60°=15°. Углы при основании АВ треугольника АВМ равны ⇒ ∆ АМВ - равнобедренный, ⇒
АМ=ВМ=22 см
Приложения:
Похожие вопросы
Предмет: Математика,
автор: zhumagulov33
Предмет: Русский язык,
автор: Аноним
Предмет: Алгебра,
автор: zarinalis937
Предмет: История,
автор: Anna218
Предмет: Химия,
автор: pirozenka4