Предмет: Геометрия,
автор: Chika2013
решение 8 задачи....
пожалуйста
Приложения:
Ответы
Автор ответа:
0
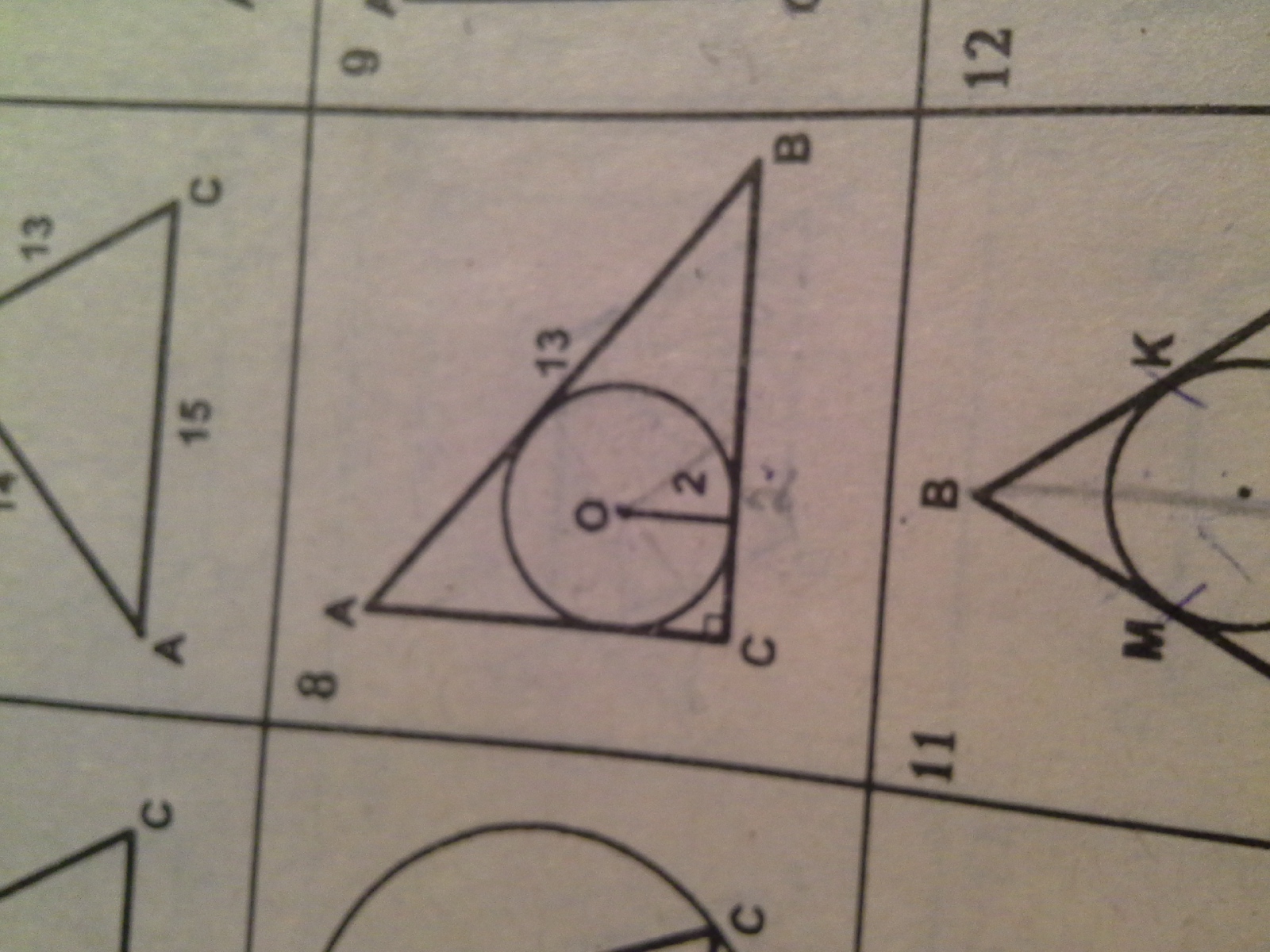
В прямоугольном треугольнике АВС гипотенуза АВ равна 13, радиус вписанной в него окружности равен 2. Найти площадь треугольника.
------
Стороны треугольника - касательные к окружности. Пусть точки касания на АС-К, на АВ-М и на ВС-Н.
По свойству отрезков касательных, проведенных из одной точки, АК=АМ, ВН=ВМ и КС=НС, эти два отрезка равны радиусу=2
Пусть ВН=х.
Тогда ВМ=х, АК=АМ=13-х.
АС=АК+КС=13-х+2=15-х
ВС=ВН+СН=х+2
По т..Пифагора
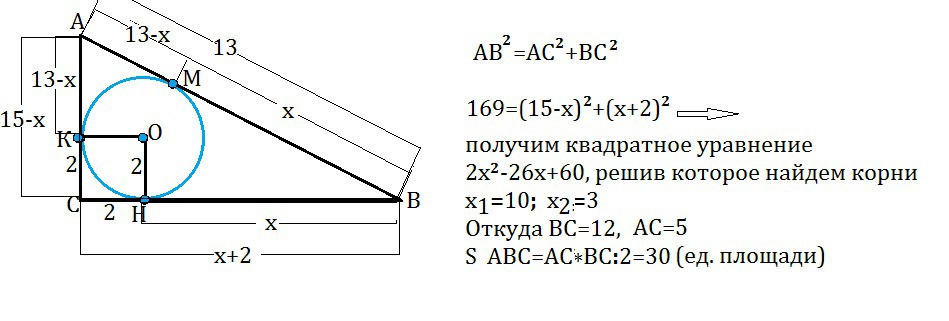
АВ²=АС²+ВС²
169=(15-х)²+(х+2)²⇒
2х²-26х+60=0
Решив квадратное уравнение, получим два корня:
х₁=10, х₂=3 ( оба подходят)
АС=5, ВС=12
S=5•12:2=30 (ед. площади)
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: kravchukanna69
Предмет: Математика,
автор: PerzikFul
Предмет: Литература,
автор: ReallyTwo
Предмет: Математика,
автор: BBlalka228