Геометрия 8-9 класс Срочноооо!!!!!!
Ответы
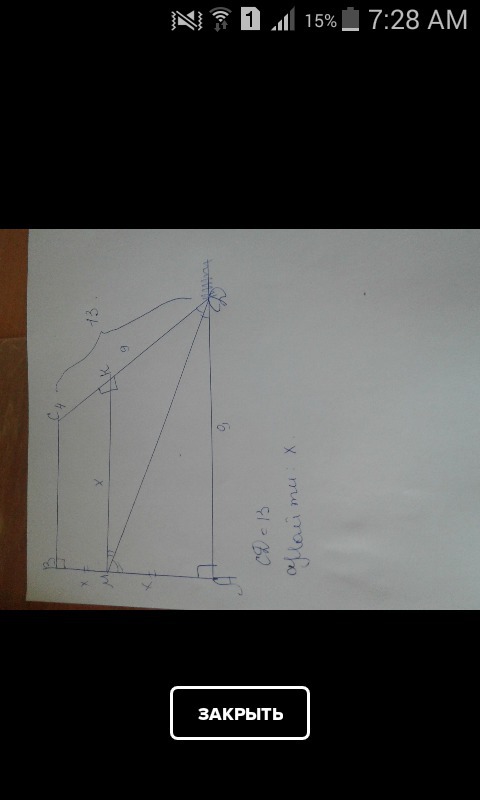
Дано: АВСД – прямоугольная трапеция;
∠А=∠В = 90⁰ ;
ДМ – биссектриса острого угла;
МК ⊥ СД;
СД = 13; АД = КД = 9;
Найти: МК; АМ; ВМ:
Решение.
1) Продолжим сторону СД лучом СЛ;
Т.к. АВСД по условию трапеция, то ВС ║ АД, а ЛД можно рассматривать как секущую: значит ∠ВСЛ = ∠АДС; тогда ∠ВСК = 180⁰ - ∠ВСЛ,
Но, т.к. четырехугольник АМКД по условию имеет 2 прямых угла, то
∠АМК = 360⁰ – 90⁰ - 90⁰ - ∠АДС , т.е. тупые углы равны: ∠АМК =∠ВСК
Четвертые (острые) углы этих четырехугольников также будут равны, т.е. ∠ ВМК = ∠АДК
Значит, четырехугольник АМКД подобен четырехугольнику ВСКМ по 4 углам, отсюда:
СК : МК = АМ : АД (1)
2) Рассмотрим ΔАМД и ΔМКД. Они не только подобны (по трем углам), но и равны, так как имеют равные стороны ( АД = КД по условию), т.е АМ = МК (2),
значит, (1) примет вид: СК : АМ = АМ : АД; (АМ)² = СК * АД
СК = СД - КД = 13 – 9 = 4;
(АМ)² = 4 * 9 = 36; АМ = √36 = 6; и МК = АМ = 6:
3) Из подобия ВСКМ и АМКД следует:
СК : ВМ = АМ : КД, откуда ВМ = (КД * СК) : АМ = (9 * 4) : 6 = 6
Ответ: МК = АМ = ВМ = 6